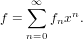10.1 OrdinaryGeneratingSeries
Definition 10.1. [BLL98, Def. 1.1.4] Consider two F-structures s1 ∈ F[U]
and s2 ∈ F[V ]. A bijection σ : U → V is called an isomorphism of s1 to s2 if
s2 = σ⋅s1 = F[σ](s1). One says that these structures have the same isomorphism
type. Moreover, an isomorphism from s to s is said to be an automorphism of
s.
Definition 10.2. [BLL98, p. 14] Let U be a set. We define an equivalence relation
∼ on F[U] by setting for s,t ∈ F[U]
In other words, s ∼ t if and only if there exists a permutation π : U → U such that
F[π](s) = t. By  we denote the isomorphism type of s.
we denote the isomorphism type of s.
Let us furthermore define
| T(Fn) | = F[n] ∕ ∼ | (120)
|
| T(F) | = ∑
n≥0T(Fn). | (121) |
Note that 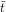 = Sn(t) is also know as the orbit of t with respect to the action
= Sn(t) is also know as the orbit of t with respect to the action
![α : Sn × F [n] → F[n], (σ,s) ↦→ F [σ ](s)](combinat225x.png) |
(122)
|
of the symmetric group Sn on F[n].
311⟨dom: OrdinaryGeneratingSeries 311⟩≡ (307)
OrdinaryGeneratingSeries: with {
⟨exports: OrdinaryGeneratingSeries 312⟩
} == FormalPowerSeries Integer add {
⟨implementation: OrdinaryGeneratingSeries 313b⟩
}
Defines:
OrdinaryGeneratingSeries, used in chunks 74, 86c, 93b, 101b, 112, 124d, 128d, 133a,
143a, 162, 169a, 177, 184, 192a, 360, 361, 628, 649, 654, 724, 725, and 729.
Uses FormalPowerSeries 242 and Integer 66.
Exports of OrdinaryGeneratingSeries
-
-
FormalPowerSeriesCategory Integer;
-
-
count: (%, MachineInteger) -> Integer Counts the number of structures of a given
size.
ToDo ⊲ 52 ⊳BUG! ⊲ 2 ⊳ mrx ⊲ 7 ⊳ 10-Feb-2007: unfortunately, without the
following chunk
Axiom complains about not finding
new. See also BUG
4.
 we denote the isomorphism type of s.
we denote the isomorphism type of s.
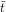 =
= ![α : Sn × F [n] → F[n], (σ,s) ↦→ F [σ ](s)](combinat225x.png)
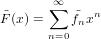
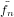 = card(
= card(