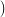8.3 The Aldor Category of Combinatorial Species
Before we come to concrete combinatorial species, we define which operations a
species should export. Therefore, we start by defining a category. Clearly, for a
combinatorial species F, we want to be able to construct for each set U the set F[U].
As explained above, we restrict the elements of U to belong to a type L. Looking
at (2), we require an Aldor function structures (see below) that should be of type
but our design uses
instead.
Note that CombinatorialSpecies and SetSpecies should be defined in the same
file since they mutually depend on each other.
We have chosen Generator instead of the probably more natural Set as the result
type, since, first, we expect that sets F[U] become so big that they might
waste more computer memory than being interesting. And, second, we want
to do ranking and unranking and thus must have a certain order on the
generated elements so that they could be deterministically mapped to natural
numbers.
As for the input, our first implementation really used Set, but in Set there
is no order of elements and thus we cannot guarantee that the resulting
generator generates structures always in the same order for identical input
sets.
The problem with Set is that sets like 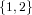 and
and 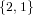 are mathematically
identical and they are also considered equal as elements of Set, but not so in
computer memory. Often sets are internally implemented as lists with the assertion
that the elements are different. No order is assumed. And it cannot be assumed since
the argument of the Set constructor is a type L that need not export an ordering
function. So internally, the above sets are represented as the lists [1,2] and [2,1],
respectively.
are mathematically
identical and they are also considered equal as elements of Set, but not so in
computer memory. Often sets are internally implemented as lists with the assertion
that the elements are different. No order is assumed. And it cannot be assumed since
the argument of the Set constructor is a type L that need not export an ordering
function. So internally, the above sets are represented as the lists [1,2] and [2,1],
respectively.
We would like the function structures return identical output for identical
input. In other words, the resulting generator would have to generate the elements in
the same order no matter whether it would be given the set 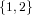 or the set
or the set 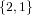 since
since
- they are identical as mathematical objects, and
- we would like to be able to speak about the n-th structure corresponding
to a certain set of labels.
Placing the labels of the n-th structure differently, gives a different structure. However,
without an ordering function we cannot bring the internal representation of 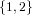 and
and 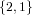 into a canonical form. That is the reason why we decided to introduce
SetSpecies.
into a canonical form. That is the reason why we decided to introduce
SetSpecies.
The domain SetSpecies is like Set, but with the additional assumption that for
a list a of type List(L) with all distinct elements taken from L and with b defined by
the equality a = b of List holds.
In order to make the function structures deterministic, we say, if x and y of
type SetSpecies(L) are two equal sets (equal in the sense of SetSpecies) and if
furthermore
-
-
(x :: List L) = (y :: List L)
then structures(x) and structures(y) are generators that generate the same
elements in the same order.
Since nothing is said about the (internal) order of elements in Set, we cannot use
Set instead of SetSpecies.
If, for example,
then x = y and
-
-
(x :: List Integer) ~= (y :: List Integer)
and thus structures(x) and structures(y) are allowed to generate the
corresponding combinatorial structures in a different order.
The function structures is the reason for putting the type L already in the
category CombinatorialSpecies.
71⟨cat: CombinatorialSpecies 71⟩≡ (55)
define CombinatorialSpecies(L: LabelType): Category == with {
⟨exports: CombinatorialSpecies 73⟩
default {
⟨defaults: CombinatorialSpecies 80⟩
}
}
Defines:
CombinatorialSpecies, used in chunks 55, 83–85, 90, 97, 107, 119, 127, 131a, 138, 147a,
166a, 175a, 182a, 191a, 194, 452, 455, 458b, 461, 626, 643–50, 652, 654, 655, 658,
and 729.
Uses LabelType 62.
What do we want to express with that category? Of course, an Aldor
category expresses the operations that are allowed for combinatorial species.
Naturally, to each combinatorial species there are associated three series, namely
8.3.1 Structures and Isomorphismtypes
Let us carry out an example that illustrates the notions of structures and
isomorphismtypes. Consider the combinatorial species L of linear orders. I.e., given a
set U of cardinality n, the species L produces all n! different linear orders of U. A
bijection σ : U V is simply a relabelling of a structure. For example, if we take
U =
V is simply a relabelling of a structure. For example, if we take
U = 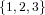 , L produces the structures L[
, L produces the structures L[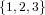 ] =
] = 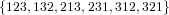 .
.
The bijection σ = 
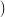 maps the structure 132 to the structure 213, thus these two structures are
isomorphic.
maps the structure 132 to the structure 213, thus these two structures are
isomorphic.
Now consider the species S of permutations. To make it more obvious that a
species takes an arbitrary set, without inherent order, set U = 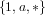 . The
structures produced by S when applied to this set are then
. The
structures produced by S when applied to this set are then
The bijection σ = 
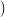 maps the structure
maps the structure 
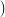 to the structure
to the structure 
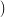 =
=

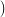 ,
which are therefore isomorphic. On the other hand, the structure
,
which are therefore isomorphic. On the other hand, the structure

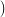 is
a fixed point of all bijections.
is
a fixed point of all bijections.
Export of CombinatorialSpecies
structures: SetSpecies L -> Generator %
Usage
s: List L := ...
for e in structures(s) repeat ...
Parameters
-
s: SetSpecies L
-
A set of labels.
Description
Generates all structures for a given set of labels.
In terms of [BLL98], this function generates the set F[U] for a species F and a finite
set U. In the Aldor implementation we have the restriction that the elements of U
must be of the same type L.
Instead of returning a Set structure, we just require being able to generate the
structures. Using Generator, we do not need to store a huge amount of data in
memory.
Export of CombinatorialSpecies
isomorphismTypes: SetSpecies L -> Generator %
Description
Generates all isomorphism types.
ToDo ⊲ 17 ⊳ rhx ⊲ 11 ⊳ 14-Aug-2006: It is not yet clear what the type of this
function/constant should be. In general, isomorphism types are equivalence classes of
structures. It could be reasonable to say that
isomorphismTypes returns
(unique) representatives of these classes. (The
unique is probably a tough
thing, since we might have no order on the input set or on
L in general.
We want to be able to use combinatorial species as labels.
80⟨defaults: CombinatorialSpecies 80⟩≡ (71)
elements(): Generator % == generate {
l: List L := empty;
for label: L in elements()$L repeat {
l := cons(label, l);
s: SetSpecies L := set reverse l;
for e: % in structures s repeat yield e;
}
}
Uses Generator 617 and SetSpecies 117.
Export of CombinatorialSpecies
expression: SpeciesExpression
Description
Returns an expression for the species.
expression returns an expression for the species, where the species itself is denoted
with the string ”Self”.
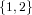 and
and 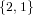 are mathematically
identical and they are also considered equal as elements of Set, but not so in
computer memory. Often sets are internally implemented as lists with the assertion
that the elements are different. No order is assumed. And it cannot be assumed since
the argument of the Set constructor is a type L that need not export an ordering
function. So internally, the above sets are represented as the lists [1,2] and [2,1],
respectively.
are mathematically
identical and they are also considered equal as elements of Set, but not so in
computer memory. Often sets are internally implemented as lists with the assertion
that the elements are different. No order is assumed. And it cannot be assumed since
the argument of the Set constructor is a type L that need not export an ordering
function. So internally, the above sets are represented as the lists [1,2] and [2,1],
respectively.
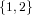 or the set
or the set 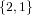 since
since
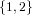 and
and 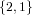 into a canonical form. That is the reason why we decided to introduce
into a canonical form. That is the reason why we decided to introduce

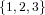 ,
, 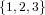 ] =
] = 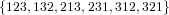 .
.

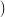
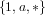 . The
structures produced by
. The
structures produced by ![{ (1 a ∗) (1 a ∗) (1 a ∗)
S[{1,a,∗}] = 1 a ∗ , 1 ∗ a , a 1 ∗ ,
( ) ( ) ( )}
1 a ∗ , 1 a ∗ , 1 a ∗ .
a ∗ 1 ∗ 1 a ∗ a 1](combinat25x.png)