Usage
Foo: FormalPowerSeriesCategory Integer with {...} == add {...}
Description
The category of formal power series.
FormalPowerSeriesCategory is the category of formal power series of the form
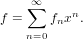 | (50) |
Let us first consider the functions that we can do with a (univariate) generating series.
The output should be piped through the following small Perl program.
sub treatBlock {
my($s)=@_; while(<>) { print "$s$_"; if (/}/) {last;} if (/{/) {treatBlock(" $s");} } } treatBlock(""); |
in order to indent the code properly.
Usage
Foo: FormalPowerSeriesCategory Integer with {...} == add {...}
Description
The category of formal power series.
FormalPowerSeriesCategory is the category of formal power series of the form
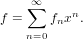 | (50) |
Exports of FormalPowerSeriesCategory
new: () -> % Creates a new uninitialized series.
new: (I -> Generator R, () -> SeriesOrder) -> % Creates a new series.
new: (I -> Generator R, SeriesOrder -> SeriesOrder, %) -> % Creates a new series from a given one.
new: (I -> Generator R, (SeriesOrder, SeriesOrder) -> SeriesOrder, %, %) -> % Creates a new series from two given ones.
0: % Returns the series (0, 0, 0,…).
1: % Returns the series (1, 0, 0,…).
monom: % Returns the series (0, 1, 0, 0,…).
term: (R, MachineInteger) -> % Creates the series (0,…, 0,r, 0,…).
coefficient: (%, MachineInteger) -> R Extracts a coefficient of the series.
coefficients: % -> Generator R Extracts all coefficient of the series.
order: % -> SeriesOrder Determines the order of the series.
approximateOrder: % -> SeriesOrder Determines a good guess of the order of the series.
zero?: % -> Boolean Zero test.
coerce: Generator R -> % Coerces a stream to a series.
coerce: DataStream R -> % Coerces a stream to a series.
coerce: % -> DataStream R Coerces a series to a stream.
set!: (%, %) -> () Destructively modifies a given series.
+: (%, %) -> % Adds two generating series.
*: (%, %) -> % Multiplies two generating series.
compose: (%, %) -> % Composes two series.
sum: Array % -> % Finite sum of series.
sum: Generator % -> % Finite or infinite sum of series.
product: Generator % -> % Finite or infinite sum of series.
if R has with {*: (Integer, %) -> %} then {
differentiate: % -> % Differentiate a series.
}
if R has with {*: (Fraction Integer, %) -> %} then {
integrate: (%, integrationConstant: R == 0) -> % Integration of a series.
}
if R has with {*: (Integer, %) -> %; *: (Fraction Integer, %) -> %} then {
exponentiate: % -> % Exponentiation of a series.
}
Export of FormalPowerSeriesCategory
new: () -> %
Description
Creates a new uninitialized series.
new() creates an uninitialized series that must be initialized by using set! before it can be used.
Remarks
Any attempt to access a coefficient of a uninitialized series results in an exception.
Export of FormalPowerSeriesCategory
new: (I -> Generator R, () -> SeriesOrder) -> %
Usage
coeffs(aord: I): Generator R == generate {
for i in 1..aord repeat yield 0;
for i in aord.. repeat yield i::R;
}
approximateOrder(): SeriesOrder == 5::SeriesOrder;
f: FormalPowerSeries(R) := new(coeffs, approximateOrder);
Description
new(coeffs, sord) creates a new series by giving a way how to generate its coefficients and how to compute an approximate order.
None of the functions coeffs or sord is evaluated before the series created by new is asked to reveal a coefficient.
The function sord is called first and its value determines the approximate order of the series f.
The function coeffs is called with the initial approximate order as its argument. The function coeffs is never called if the initial approximate order turns out to be infinity.
Export of FormalPowerSeriesCategory
new: (I -> Generator R, SeriesOrder -> SeriesOrder, %) -> %
Usage
g: Generator Integer := generate {
for z: Integer in 1.. repeat yield z*(z+1);
}
f := g :: FormalPowerSeries(Integer);
shift(x: %)(aord: I): Generator Integer == generate {
for i in 1..aord repeat yield 0;
for i in aord.. repeat yield coefficient(x, i-1);
}
f: FormalPowerSeries(Integer) == new(shift x, increment, x);
Description
Creates a new series from a given one.
new(coeffs, sord, x) creates a new series by giving a way how to generate its coefficients and how to compute an approximate order from the approximate order of the given series.
None of the functions coeffs or sord is evaluated before the series created by new is asked to reveal a coefficient.
The function sord is called first and its value determines the approximate order of the series f.
The function coeffs is called with the initial approximate order as its argument. The function coeffs is never called if the initial approximate order turns out to be infinity.
Export of FormalPowerSeriesCategory
new: (I -> Generator R, (SeriesOrder, SeriesOrder) -> SeriesOrder, %, %) -> %
Usage
plus(x: %, y: %)(aord: I): Generator R == generate {
for n: I in 1..aord repeat yield 0@R;
for n: I in aord.. repeat yield coefficient(x, n) + coefficient(y, n);
}
f: FormalPowerSeries(Integer) := new(plus(x, y), min, x, y);
Description
Creates a new series from two given ones.
new(coeffs, sord, x, y) creates a new series by giving a way how to generate its coefficients and how to compute an approximate order from the approximate orders of the given series.
None of the functions coeffs or sord is evaluated before the series created by new is asked to reveal a coefficient.
The function sord is called first and its value determines the approximate order of the series f.
The function coeffs is called with the initial approximate order as its argument. The function coeffs is never called if the initial approximate order turns out to be infinity.
Export of FormalPowerSeriesCategory
0: %
Description
Returns the series (0,0,0,…).
In this context 0 corresponds to the series
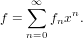 | (51) |
The coefficients are equal to the coefficients of term(0, 0).
The order of this series is infinity.
Export of FormalPowerSeriesCategory
1: %
Description
Returns the series (1,0,0,…).
In this context 1 corresponds to the series
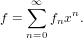 | (52) |
The coefficients are equal to the coefficients of term(1, 0).
Export of FormalPowerSeriesCategory
monom: %
Description
Returns the series (0,1,0,0,…).
The constant monom corresponds to the series
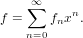 | (53) |
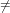 1 and f1 = 1.
1 and f1 = 1.
The coefficients are equal to the coefficients of term(1, 1).
Export of FormalPowerSeriesCategory
term: (R, MachineInteger) -> %
Usage
r: Integer := 7;
n: MachineInteger := 3;
term(r, n);
Description
Creates the series (0,…,0,r,0,…).
The function call term(r, n) creates the term rxn considered as a series.
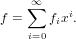 | (54) |
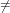 n and fn = r.
n and fn = r.
Special cases are given by 1, which is equal to term(1, 0), and monom, which is equal term(1, 1).
Export of FormalPowerSeriesCategory
coefficient: (%, MachineInteger) -> R
Usage
T == Integer;
S == FormalPowerSeries T;
import from DataStream T;
s: S := stream(generator [1,2,3,4,0]) :: S;
c := coefficient(s, 3);
d := coefficient(s, 9);
Description
Extracts a coefficient of the series.
For a series
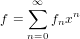 | (55) |
Since series are 0-based c = 4 and d = 0 in the above example.
Export of FormalPowerSeriesCategory
coefficients: % -> Generator R
Usage
T == Integer;
S == FormalPowerSeries T;
import from DataStream T;
s: S := stream(generator [7,5,7,4,0]) :: S;
l: List T := [x for i in 1..9 for x in coefficients s];
Description
Extracts all coefficient of the series.
For a series
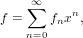 | (56) |
In the above example the list l will be equal to [7,5,7,4,0,0,0,0,0].
Export of FormalPowerSeriesCategory
order: % -> SeriesOrder
Usage
f: FormalPowerSeries Integer := ...
o: SeriesOrder := order f;
o = unknown => {... order is not yet computed ...}
o = infinity => {... f=0 ...}
n: MachineInteger := o :: MachineInteger;
Description
Determines the order of the series.
For a series
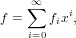 | (57) |

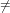
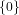 , the call order(f) does not return unknown, but rather the true
order n of the series f. If o = n ≥ 0 then fn
, the call order(f) does not return unknown, but rather the true
order n of the series f. If o = n ≥ 0 then fn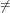 0 and fi = 0 for all i < n, i. e.,
0 and fi = 0 for all i < n, i. e.,
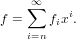 | (58) |
Export of FormalPowerSeriesCategory
approximateOrder: % -> SeriesOrder
Usage
f: FormalPowerSeries Integer := ...
ao: SeriesOrder := approximateOrder f;
assert(ao ~= unknown);
ao = infinity => {... f=0 ...}
n: MachineInteger := ao :: MachineInteger;
Description
Determines a good guess of the order of the series.
For a series
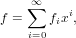 | (59) |
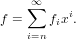 | (60) |
Remarks
It might happen that the function returns different values when called on the same series. For example, a1 at one time and a2 at a later point in time. In accordance with the specification above, it holds a1 ≤ a2.
l: List Integer := [0,0,0,0,4,0];
s: DataStream := stream generator l;
f: FormalPowerSeries(Integer) := s :: FormalPowerSeries(Integer);
a1: SeriesOrder := approximateOrder(f);
assert(0 = a1 :: MachineInteger);
z: Integer := coefficient(f, 2);
assert(zero? z);
a2: SeriesOrder := approximateOrder(f);
assert(2 = a2 :: MachineInteger);
z: Integer := coefficient(f, 20);
assert(zero? z);
a3: SeriesOrder := approximateOrder(f);
assert(4 = a3 :: MachineInteger);
Export of FormalPowerSeriesCategory
zero?: % -> Boolean
Usage
T == Integer;
S == FormalPowerSeries T;
import from DataStream T;
s: S := stream(generator [0,2,3,4,0]) :: S;
b1: Boolean := zero? s;
s := 0;
b2: Boolean := zero? s;
s := stream(generator [0]) :: S;
b3: Boolean := zero? s;
i0: Integer := coefficient(s, 0);
b4: Boolean := zero? s;
i1: Integer := coefficient(s, 1);
b5: Boolean := zero? s;
Description
Zero test.
The function call zero?(s) returns true if s is known to be the zero series. It returns false if s is different from zero or it is not known that s is the zero series.
Remarks
Export of FormalPowerSeriesCategory
coerce: Generator R -> %
Usage
T == Integer;
g: Generator T := generate for i in 0.. repeat yield i*i;
u := g :: FormalPowerSeries(T);
Description
Coerces a stream to a series.
For a generator g which generates f0,f1,f2,…, the call coerce(g) constructs the series
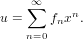 | (61) |
Export of FormalPowerSeriesCategory
coerce: DataStream R -> %
Usage
T == Integer;
g: Generator T := generate for i in 0.. repeat yield i*i;
s: DataStream T := stream g;
u := s :: FormalPowerSeries(T);
Description
Coerces a stream to a series.
For a stream s = (f0,f1,f2,…), the call coerce(s) constructs the series
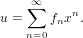 | (62) |
Export of FormalPowerSeriesCategory
coerce: % -> DataStream R
Usage
T == Integer;
g: Generator T := generate for i in 0.. repeat yield i*i;
s: DataStream T := stream g;
u := s :: FormalPowerSeries(T);
Description
Coerces a series to a stream.
For a series
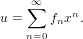 | (63) |
Export of FormalPowerSeriesCategory
set!: (%, %) -> ()
Usage
import from Integer;
s: FormalPowerSeries Integer := new();
set!(s, 1 + monom * s * s);
l1: List Integer := [1,1,2,5,14,42];
l2: List Integer := [x for i in l1 for x in coefficients s];
Description
Destructively modifies a given series.
This function is particularly useful for the definition of series that are defined in a recursive way.
Since addition and multiplication of series is lazy, the construction of
does not compute any coefficient of the series s.The two lists l1 and l2 from the example code above are equal.
Export of FormalPowerSeriesCategory
+: (%, %) -> %
Usage
import from Integer;
s: FormalPowerSeries Integer := new();
set!(s, 1 + monom * s * s);
l1: List Integer := [1,1,2,5,14,42];
l2: List Integer := [x for i in l1 for x in coefficients s];
Description
Adds two generating series.
Let
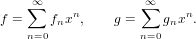 | (64) |
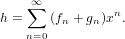 | (65) |
Export of FormalPowerSeriesCategory
*: (%, %) -> %
Usage
import from Integer;
s: FormalPowerSeries Integer := new();
set!(s, 1 + monom * s * s);
l1: List Integer := [1,1,2,5,14,42];
l2: List Integer := [x for i in l1 for x in coefficients s];
assert(l1=l2);
ones: FormalPowerSeries Integer := series stream 1;
pos: FormalPowerSeries Integer := ones * ones;
m1: List Integer := [1,2,3,4,5,6,7];
m2: List Integer := [x for i in m1 for x in coefficients pos];
assert(m1=m2);
Description
Multiplies two generating series.
Let
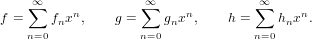 | (66) |
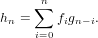 | (67) |
Export of FormalPowerSeriesCategory
compose: (%, %) -> %
Usage
macro S == FormalPowerSeries Integer;
import from Integer;
s: S := stream(1) :: S;
t: S := stream(generator [0,0,1]) :: S;
u := compose(s, t);
l1: List Integer := [1, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34];
l2: List Integer := [x for i in l1 for x in coefficients u];
assert(l1 = l2);
Description
Composes two series.
Let
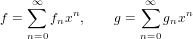 | (68) |
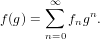 | (69) |
Export of FormalPowerSeriesCategory
sum: Array % -> %
Usage
macro {
Z == Integer;
S == FormalPowerSeries Z;
}
s: S := stream(1) :: GS;
a: Array S := [s,s,s,s,s,s];
l1: List Z := [6,6,6,6,6,6,6,6,6,6];
l2: List Z := [x for i in l1 for x in coefficients sum g];
assert(l1=l2);
Description
Finite sum of series.
Let a = (s0,s1,s2,…,sm) be a finite tuple of formal power series. The call sum(a) returns a formal power series
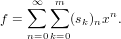 | (70) |
Remarks
The behaviour of the function is undefined if the input array is of length 0.
Export of FormalPowerSeriesCategory
sum: Generator % -> %
Usage
macro {
Z == Integer;
S == FormalPowerSeries Z;
}
s: S := stream(1) :: GS;
g: Generator S := s for n in 0..5;
l1: List Z := [1,2,3,4,5,6,6,6,6,6];
l2: List Z := [x for i in l1 for x in coefficients sum g];
assert(l1=l2);
Description
Finite or infinite sum of series.
Let g = (g0,g1,g2,g3,…) be a finite or infinite sequence of formal power series. For simplicity, we extend a finite sequence into an infinite one by adding zero series. However, we do not allow g to generate nothing at all.
The call sum(g) returns a formal power series
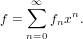 | (71) |
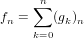 | (72) |
Remarks
The way in which we defined f basically says that f = ∑ k=0∞gk if ord(gn) ≥ n. Although theoretically for finite sequences g = (g0,g1,…,gn) the order condition would not be necessary, we must require it, since there is no way to figure out in advance whether the given sequence g is, in fact, finite.
The behaviour of the function is undefined if input generator does not generate any element.
Export of FormalPowerSeriesCategory
product: Generator % -> %
Usage
macro {
Z == Integer;
S == FormalPowerSeries Z;
}
s: S := stream(1) :: GS;
g: Generator S := s for n in 0..5;
l1: List Z := [1,2,3,4,5,6,6,6,6,6];
l2: List Z := [x for i in l1 for x in coefficients product g];
assert(l1=l2);
Description
Finite or infinite sum of series.
Let g = (g0,g1,g2,g3,…) be a finite or infinite sequence of formal power series. For simplicity, we extend a finite sequence into an infinite one by adding zero series. However, we do not allow g to generate nothing at all.
The call product(g) returns a formal power series
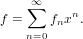 | (73) |
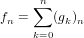 | (74) |
Remarks
The way in which we defined f basically says that f = ∑ k=0∞gk if ord(gn) ≥ n. Although theoretically for finite sequences g = (g0,g1,…,gn) the order condition would not be necessary, we must require it, since there is no way to figure out in advance whether the given sequence g is, in fact, finite.
The behaviour of the function is undefined if input generator does not generate any element.
Export of FormalPowerSeriesCategory
differentiate: % -> %
Usage
Description
Differentiate a series.
Let
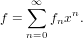 | (75) |
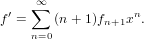 | (76) |
Export of FormalPowerSeriesCategory
integrate: (%, integrationConstant: R == 0) -> %
Usage
Description
Integration of a series.
Let
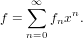 | (77) |
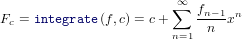 | (78) |
set!, +, *, differentiate
Export of FormalPowerSeriesCategory
exponentiate: % -> %
Usage
Description
Exponentiation of a series.
Let
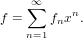 | (79) |
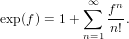 | (80) |
set!, +, *, differentiate, integrate