4.3 Mathematical Notation
In this section we are going to defines some mathematical notation that is used in
the document.
4.3.1 Common Sets
The common sets of natural numbers, integers, rationals, reals, and complex numbers
are defined below. Furthermore we define some notation specific to combinatorial
species.
25⟨mathematics 25⟩≡ (20) 26 ⊳
\newcommand{\setFont}{\protect\mathbb}
\newcommand{\fieldFont}{\protect\mathbb}
\newcommand{\setC}{\setFont{C}} % complex numbers
\newcommand{\setN}{\setFont{N}} % natural numbers
\newcommand{\setQ}{\setFont{Q}} % rational numbers
\newcommand{\setR}{\setFont{R}} % real numbers
\newcommand{\setZ}{\setFont{Z}} % integers
\newcommand{\fieldK}{\fieldFont{K}}
\newcommand{\category}{\protect\mathbb}
\newcommand{\categoryFiniteSet}{\category{E}}
\newcommand{\categoryE}{\categoryFiniteSet} % abbreviation
\newcommand{\categoryBijectiveFiniteSet}{\category{B}}
\newcommand{\categoryB}{\categoryBijectiveFiniteSet} %abbreviation
Uses Q 47 and Z 47.
4.3.2 Set Notation
In order to get the size of braces correct in set definitions, we provide the following
commands.
26⟨mathematics 25⟩+
≡ (20) ⊲25 28a ⊳
\newcommand{\Set}[1]{\left\{#1\right\}}
\newcommand{\setDef}[2]{{#1}\left|\,\vphantom{#1}{#2}\right.}
\newcommand{\SetDef}[2]{\Set{\,\setDef{#1}{#2}\,}}
Then we have
- $\Set{a,b,c}$
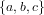
- $\Set{\Set{a,b},c}$
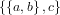
- \[\Set{\Set{a,b},c}\]
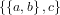
- $\Set{a,\frac{b}{c}}$
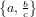
- \[\Set{a,\frac{b}{c}}\]
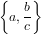
- $\SetDef{\int_{a}^\infty f(x) dx}{a\in\Set{3,4,5}}$
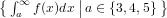
- \[\SetDef{\int_{a}^\infty f(x) dx}{a\in\Set{3,4,5}}\]
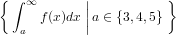
The power set of a set X is denoted by P(X).
28a⟨mathematics 25⟩+
≡ (20) ⊲26 28b ⊳
\newcommand{\PowerSet}[1]{\ensuremath{\protect\mathcal{P}(#1)}}
With 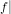 U we denote the restriction of some function f to a subset U of its
original source domain.
U we denote the restriction of some function f to a subset U of its
original source domain.
28b⟨mathematics 25⟩+
≡ (20) ⊲28a 28c ⊳
\newcommand{\restrictedTo}[2]{\left.#1\right|_{#2}}
4.3.3 Math-Operators
Not all mathematical operators are defined in the amsmath package, so we define here
a few more.
28c⟨mathematics 25⟩+
≡ (20) ⊲28b 28d ⊳
\DeclareMathOperator{\card}{card} % set cardinality
\DeclareMathOperator{\ord}{ord} % order of a series
\DeclareMathOperator{\supp}{supp} % support of a polynomial
\DeclareMathOperator{\fix}{fix} % number of fixed points
\DeclareMathOperator{\Fix}{Fix} % the fixed elements
\DeclareMathOperator{\aut}{aut} % aut k = 1^{k_1}k_1! ... n^{k_n}k_n!s
\DeclareMathOperator{\lcm}{lcm} % least common multiple
4.3.4 Functorial Composition
The following definition is used for denoting the functorial composite F ⊓ ⊔ G of two
species F and G.
28d⟨mathematics 25⟩+
≡ (20) ⊲28c 29 ⊳
\def\functorialcompose{\mathbin{\rlap{$\sqcap$}\sqcup}}
4.3.5 Theorem-like Environments
29⟨mathematics 25⟩+
≡ (20) ⊲28d
\usepackage{amsthm}
\theoremstyle{plain}
\newtheorem{Theorem}{Theorem}[section]
\newtheorem{Lemma}[Theorem]{Lemma}
\newtheorem{Corollary}[Theorem]{Corollary}
\newtheorem{Example}[Theorem]{Example}
\newtheorem{Proposition}[Theorem]{Proposition}
% Can have an argument in square brackets (Proof name).
\newenvironment{Proof}{\begin{proof}}{\end{proof}}
\newtheorem{Problem}{Problem}
\theoremstyle{remark}
\newtheorem{Remark}[Theorem]{Remark}
\theoremstyle{definition}
\newtheorem{Definition}[Theorem]{Definition}
Uses name 198.
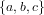
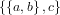
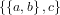
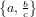
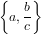
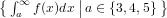
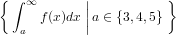
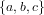
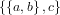
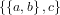
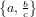
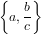
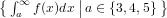
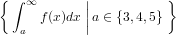
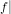 U we denote the restriction of some function f to a subset U of its
original source domain.
U we denote the restriction of some function f to a subset U of its
original source domain.