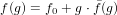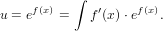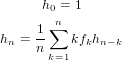9.2 FormalPowerSeries
This domain implements the ring R[[x]] of formal power series over a ring
R.
For a greater range of applicability, our Aldor implementation only requires that
R provides ring-like operations, i. e., R must only satisfy ArithmeticType.
A formal power series f is an infinite formal sum of the form:
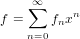 |
(81)
|
with coefficients fn being elements of a certain ring R.
A series is basically a stream of elements of R. However, we want to be able to
deal with code like the following.
And we want that the two lists l1 and l2 agree.
Note that the series equation actually is s = x + s2 which, in fact, has two
solutions.
| s1 | =  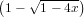 = x + x2 + 2x3 + 5x4 + 14x5 + O(x6) = x + x2 + 2x3 + 5x4 + 14x5 + O(x6) | (82)
|
| s2 | =  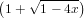 = 1 − x − x2 − 2x3 − 5x4 − 14x5 + O(x6) = 1 − x − x2 − 2x3 − 5x4 − 14x5 + O(x6) | (83) |
For applications in generating series, we are only interested in series with
non-negative coefficients. Since we cannot test infinitely many coefficients we choose
one of the series by another method. We simply take the one that has the biggest
order.
In fact, such an approach is reasonable in order to help prevent infinite recursion.
Note that in our design we never see the whole defining series equation. All that we
can build on are data structures and the local operators + and *. So we cannot invoke
a solver that returns the radical expression and from there generate the
series.
We do not want to invoke any solver at all, not even one that works on elements
of R in order to solve for the first few coefficients of the series. Thus we first try to
figure out from the local data what the biggest possible order would be so that the
series still fulfils the equation.
To do that algorithmically, we first assume an unknown order an
try to adjust it at the operator places. In fact, to break recursion, it is
sufficient to work with an approximate order. An approximate order of a
series is either unknown or it is smaller or equal to the true order of the
series.
So internally, we store an approximate order and the true order of the series. Initially,
(except for certain series like 0 or 1) these values are set to unknown. If the first
coefficient needs to be accessed, the approximate order is computed (and not earlier).
The true order is then figured out starting from the approximate order and checking
already accessed elements.
Convention ⊲ 2 ⊳ In no case is the order computation allowed to step
the generator that is stored insided the stream from the representation.
Another example that we want to be able to deal with is given by the following
code.
This example corresponds to the system
| s | = 1 + xt3 | (84)
|
| t | = 1 + xs2 | (85) |
for the series s and t.
Note that from this example it becomes clear that our implementation must be
fully lazy, since at the time we define s in the program, there is no information about
t. Every compuation has to be postponed until the series is asked to reveal one of its
coefficients.
ToDo ⊲ 38 ⊳ rhx ⊲ 28 ⊳ 12-Sep-2006: Add a proof that under certain conditions
there is only one such sequence with maximal order.
Type Constructor
FormalPowerSeries
Usage
macro R == Integer;
f: FormalPowerSeries R := 1 + monom + term(-1, 2);
Description
Series with integer coefficients.
FormalPowerSeries is the domain that represents series with integer coefficients,
i. e., formal series f of the form
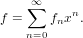 |
(86)
|
with
fi ∈ R for all
i ≥ 0.
242⟨dom: FormalPowerSeries 242⟩≡ (196)
FormalPowerSeries(R: ArithmeticType): FormalPowerSeriesCategory R == add {
macro {
X == rep x;
Y == rep y;
T == rep t;
}
⟨representation: FormalPowerSeries 245⟩
import from R, Rep, I, SeriesOrder;
⟨TRACE: FormalPowerSeries 243⟩
⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩
⟨implementation: FormalPowerSeries 261⟩
}
Defines:
FormalPowerSeries, used in chunks 112, 311, 314, 316, 321b, 330, and 685.
Uses FormalPowerSeriesCategory 199, I 47, and SeriesOrder 289.
243⟨TRACE: FormalPowerSeries 243⟩≡ (242)
#if TRACE
name(x: %): String == X.TRACENAME;
setName!(s: String)(x: %): % == {X.TRACENAME := s; x}
trace(x: %): String == {
import from SeriesOrder, Boolean;
s: StringBuffer := new();
tw := s :: TextWriter;
tw << name(x) << " [" << X.order;
tw << "," << X.approximateOrder;
tw << "," << X.approximateOrderChanged? << ",";
if initialized? x then {
tw << "#" << #(X.coefficientStream);
} else {
tw << "?"
}
tw << "]";
string s;
}
macro SETNAME(s)(x) == setName!(s)(x);
#else
macro SETNAME(s)(x) == x;
#endif
macro TRACEFPS(fn, text, z) == TRACE(fn + " " + text + ": ", trace z);
Defines:
SETNAME, used in chunks 263b, 264a, 268, 269a, 272, 273a, 275b, 278b, 281a, 283, 285b,
332, 342, 345b, 361, and 363.
TRACEFPS, used in chunks 251, 255, 257–61, 265, 266a, and 281b.
Uses approximateOrderChanged? 245, coefficientStream 245, initialized? 249b,
name 198, SeriesOrder 289, setName! 198, String 65, and TRACENAME 245.
Our implementation, in fact, creates a new series for every operation. So for
it creates one series for * and one series for +. The series for monom is a constant. The
series s is identical to the one created by +.
Similarly, for
Two (different) series for the two * operations will be created and one series for the +
operation. The latter one is identical to s.
That seems to be a waste of memory, but it basically saves intermediate results,
that would have to be recomputed otherwise.
If any improvement with respect to memory consumption is started later, one
should take care not to remove the structure that stores the approximate order of
these auxiliary series.
The approximate order is heavily used to avoid recursion in the above examples.
Basically, before any coefficient is accessed, an approximate order is computed for
every series involved in the expression.
If we abbreviate x = monom, we can write the second example as:
| s | = 1 + v, | u | = x ⋅ s, | v | = u ⋅ s | (87) |
Since the (approximate) orders of 1 and x are known to be ord(1) = 0 and
ord(x) = 1, the approximate orders of s, u, and v (here also denoted by ord) are
computed to be:
| ord(s) | = 0, | ord(u) | = 1, | ord(v) | = 1. | (88) |
Now if s0 is to be computed, we have to compute 10 + v0. We know that
10 = 1. Since we have precomputed the approximate order of v, we know that
v0 = 0, so we can skip its actual computation without recursing through u and
s.
9.2.1 Representation
Note that if the following data structure is changed, the function set! must be
changed appropriately.
245⟨representation: FormalPowerSeries 245⟩≡ (242)
Rep == Record(
#if TRACE
TRACENAME: String,
#endif
order: SeriesOrder,
approximateOrder: SeriesOrder,
approximateOrderChanged?: Boolean,
computeApproximateOrder!: % -> (),
initializedCoefficients?: Boolean,
coefficientStream: DataStream R
);
macro BRACKET(o, ao, c?, cao, i?, c) == per [
#if TRACE
"??",
#endif
o, ao, c?, cao, i?, c];
Defines:
approximateOrderChanged?, used in chunks 243, 257, 258, 260, 262–65, and 270a.
BRACKET, used in chunks 262–64 and 270a.
coefficientStream, used in chunks 243, 253a, 259b, 262–67, and 270a.
initializedCoefficients?, used in chunks 249b, 259b, 262–65, and 270a.
TRACENAME, used in chunks 243 and 265b.
Uses DataStream 386, SeriesOrder 289, and String 65.
We have the following possible meanings:
|
|
|
| order | approximateOrder | meaning |
|
|
|
| unknown | unknown | order is not yet computed |
| unknown | n ≥ 0 | order is computed but not verified |
| unknown | ∞ | should never happen |
| ∞ | ∞ | the series is zero |
| n ≥ 0 | n ≥ 0 | series is non-zero |
|
|
|
| |
A value of unknown stored in approximateOrder should trigger computation of an
approximate order. But it should trigger the computation only if it is necessary to get
the real value of a coefficient of the series.
The value unknown is returned from the function order to the user if it is not yet
known what the (true) order of the series is. If an approximate order has been
computed then each invocation of the function coefficient triggers an
attempt to improve the approximate order until the true order has been
found.
If for a series f the value for approximateOrder is a non-negative number n, then
it is assured that the series coefficients are zero for all indicies smaller than n, in
other words the series can be written in the form
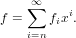 |
(89)
|
The entry stored in order is either unknown or equal to what is stored in
approximateOrder.
An unknown order corresponds
(nearly )
to ∞ with respect to arithmetic, but there is only one series for which ∞ would, in
fact, be the correct value, that is the 0 series.
Note that we do not say that the value stored in approximateOrder is the true
order of the series f. It is still possible that fn = 0. For our purpose the computation
of a sufficiently big n is, however, enough.
In fact, if we know the approximate order of two non-zero series s and t then the
approximate order of operations on s and t is given by the following equations. (We
abbreviate approximateOrder by ord.)
Note that in general, for the sum of series it only holds the inequality with a ≥
sign in (90). We are, however, completely satisfied with taking (90) as the definition
of an approximate order of the sum of two series, since all we need is to prevent
infinite recursion.
For integration we actually take also a non-zero integration constant into
account.
9.2.2 Initialization of the Representation
Recall Convention 2. Operations on series like + or * do not trigger the
computation of the (approximate) order of the resulting series. In fact, such
operations must not do any series compuation at all, since for series which
are recursively defined by an equation system, we might not have enough
information to do the order computation correctly. Only when a coefficient is
needed the computation is triggered and the full computation is never done
twice.
The initialization process works in two phases.
- Build the representation record with some uninitialized data.
- Right before the first coefficient is accessed, the approximate order is
computed and the coefficient stream is initialized.
In fact, we delay not only the order computation until a coefficient is needed, but
even the computation of the stream of coefficients is delayed. Since we have to put
something in the representation at the place where the coefficient stream is stored, we
decided to put the empty stream.
Whether or not the field coefficientStream is uninitialized, should correspond to the
value stored in the field initializedCoefficients?.
Via that field we make sure that the initialization, i. e., the computation of an
approximate order and the actual compuation of the coefficient stream is done only
once.
The following function initialize! is an auxiliary function that is called at the
beginning of the function zero? (cf. Section 9.2.4) and (through the call to zero?
also in the function coefficient) in order to compute an approximate order of the
series, to improve a previously computed order, and to set the true order if it can be
verified that the approximate order is the true order of the series. In fact, the
function is called any time before a coefficient is accessed in order to make sure
everything is properly set.
The initialization roughly works as follows.
- If the order of the series is known, then nothing has to be done since in that
case it is assumed that the coefficient stream has already been initialized.
In that case also the approximate order must be known. Nothing must be
done.
- If the approximate order is known, then (at the time initialize! is
called) also the coefficient stream must already have been initialized. In
that case we can try to improve the approximate order and possibly set
the true order of the series.
- If nothing is known, the actual initialization is started. It first computes
an approximate order and then initializes the coefficient stream.
All this is done via the function
computeApproximateOrder!(x) .
With the help of the functions approximateOrder!, new, and set! a recursive
approximation of the order can be done. A very important fact is that
for the function computeApproximateOrder! it can happen that the
approximate order is set to something different than unknown and
at the same time the coefficient stream is uninitialized. In particular
that happens for recursive definitions of streams like the following.
251⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩+
≡ (242) ⊲250 255 ⊳
local initialize!(x: %): () == {
TRACEFPS("initialize!", "B", x);
X.order ~= unknown => return; -- nothing to do
ao: SeriesOrder := X.approximateOrder;
assert(ao ~= infinity); -- because order would be equal to infinity
ao ~= unknown => {⟨try to improve the approximate order ao 253a⟩}
assert(not initialized? x);
computeApproximateOrder! x;
TRACEFPS("initialize!", "E", x);
assert(initialized? x);
}
Uses computeApproximateOrder! 250, initialized? 249b, SeriesOrder 289,
and TRACEFPS 243.
Before we come to the function computeApproximateOrder!, let us deal with the
case where an approximate order is known and we need to verify whether the
approximate order is, in fact, the true order of the series. The code below does this
by testing whether the entry in the position given by the approximate order is really
non-zero. If that is the case, it changes the order entry in the representation from
unknown to the approximate order. If it is not the case, the approximate order can be
increased by 1 and another check is done. According to Convention 2, this iteration
can only be done for the finitely many elements of the series that have already been
accessed. If this iteration does not recognize the true order of the series, we
wait for the next call to initialize! to improve the approximate order
further.
We have chosen such a stepwise approach since x might be the zero series coming,
for example, from
For such a series initialize! would not terminate while trying to improve the
approximate order. See also the implementation of the function coerce in
FormalPowerSeries as given in Section 9.2.5.
To check the true order, we must access elements of the given series without
violating Convention 2. The computation of the order should in no case start the
generator that is stored inside the stream of the series, order computation is,
however, allowed to access elements of the stream that are already computed, i. e., for
a series x and
it is allowed to call
for any n < #s.
Note that, in case we have realized that the series is the zero series, the order and
the approximate order have been set to infinity. Thus if we know that
the order is unknown then we also know that the approximate order is not
infinity.
253a⟨try to improve the approximate order ao 253a⟩≡ (251)
i: I := ao :: I;
c: DataStream R := X.coefficientStream;
n: I := #c;
TRACE("number of cached values = ", n);
i >= n => {⟨try to recognize the zero series 253b⟩}
while i < n and zero? c.i repeat {
TRACE("verifyOrder! zero i = ", i);
i := next i;
X.approximateOrder := i :: SeriesOrder;
}
if i < n then { -- "if not zero? c.i" might be more costly
TRACE("verifyOrder! non-zero i = ", i);
X.order := i :: SeriesOrder;
}
Uses coefficientStream 245, DataStream 386, I 47, and SeriesOrder 289.
To recognize the zero series is only possible if we detect that the underlying
stream is constant. If that is the case and the last computed value is 0, then we know
we have the zero series, since we only run the following code if all values at entries
less than the current approximate order are 0.
253b⟨try to recognize the zero series 253b⟩≡ (253a)
TRACE("Constant stream?: ", constant? c);
not constant? c => return; -- for non-constant series we cannot do anything
assert(zero?(c.(prev #c)));
X.approximateOrder := infinity;
X.order := infinity;
Note that we do not need to test anymore whether the constant value is zero. Either
the approximate order is already bigger than #(c) or it has been increased one by one
in previous invocations of initialize!.
9.2.3 Computation of an Approximate Order
Let us describe how to compute an approximate order if it has not yet been
done.
Our representation data structure (see Section 9.2.1) contains an entry
-
-
computeApproximateOrder!: % -> ()
which is used for the computation of an approximate order if it is needed. How
the approximate order should be computed, is stored in that entry. This
function computes a new approximate order. It can make use of the entry
-
-
approximateOrderChanged?: Boolean
in the representation. That entry is initially set to true and is particularly
useful to avoid infinite recursion while computing an approximate order
in recursively defined series as given, for example, in the following code.
In particular the function approximateOrder! uses that entry in a non-trivial way.
Basically, the computation recurses until the approximate order does not change
anymore.
Let us now describe functions that could be stored in the representation data
structure at computeApproximateOrder!. We allow the following functions.
-
doNothing:
- The function does nothing at all. It is a dummy function for cases
where an (approximate) order is known at creation time of the series.
-
uninitialized:
- The function is an auxiliary function for the definition of an
uninitialized power series through the function new. This function raises
an exception when called.
-
approximateOrder!:
- This function (or rather these functions, since there is a
nullary, unary, and binary version) computes a new approximate order
from approximate orders of its arguments. It should be understood as a
wrapper function around the functions such as + and * from SeriesOrder
which takes care of recursively defined series.
For some series there is no need to do an order computation at all, since the order
is already known at creation time. Examples are given by the implementation of the
series 0, 1, monom, and term in Section 9.2.5.
255⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩+
≡ (242) ⊲251 257 ⊳
local doNothing(x: %): () == {
TRACEFPS("doNothing", "|", x);
assert(X.approximateOrder ~= unknown);
assert(initialized? x);
}
Uses initialized? 249b and TRACEFPS 243.
Now we consider the complicated part of the order computation of the function
initialize!, namely the function approximateOrder!. There is a nullary, unary,
and binary version of that function. Since their implementation is very similar, we
only describe the binary version.
This function computes a new approximate order from approximate orders of its
arguments. It should be understood as a wrapper function around the functions such
as + and * from SeriesOrder which takes care of recursively defined series. Functions
such as + and * appear as the argument newOrder in the function declaration below.
For understanding of how the function approximateOrder! is used, look, for
example, into the definition of + in Section 9.2.8 and at the implementation of
new.
For some series we can compute the approximate order according to equations
(90) and (91). That holds in particular for the sum and product of series, cf.
Sections 9.2.8 and 9.2.11, respectively.
The basic idea for approximateOrder! is that initially it sets all unknown
approximate orders (of series involved in the definition of the series in question) to
infinity and then (according to the structure of the equation that defines the
series) tries to improve that initial guess by drawing conclusions from the guess
and equations such as given by (90) and (91) until a stabilized situation is
achieved.
We should add a note here about the fact that approximateOrder! does not only
compute an approximate order, but (in case at invocation time the approximate
order was unknown) it also initializes the coefficient stream. Thus, if the
coefficient stream is known to be initialized, then there is no need to do the
computation of the approximate order again. The follwing are invariants of
approximateOrder!.
As can be seen from the code below, if initializeCoefficientStream! is called,
the approximate orders of x, y, and t have already been properly computed.
257⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩+
≡ (242) ⊲255 258 ⊳
local approximateOrder!(
computeCoefficients: I -> Generator R,
newOrder: (SeriesOrder, SeriesOrder) -> SeriesOrder,
x: %,
y: %
)(t: %): () == {
TRACEFPS("approximateOrder2!", "{ t", t);
TRACEFPS("approximateOrder2!", "x", x);
TRACEFPS("approximateOrder2!", "y", y);
initialized? t => {TRACEFPS("approximateOrder2!", "i}", t); return}
ochanged?: Boolean := T.approximateOrderChanged?;
mustInitializeCoefficientStream? := T.approximateOrder = unknown;
macro aOrd(x, y) == newOrder(X.approximateOrder, Y.approximateOrder);
ao: SeriesOrder := aOrd(x, y);
if ao = unknown then ao := infinity; -- start at maximum
tchanged?: Boolean := setApproximateOrder!(t, ao);
if ochanged? or tchanged? then {
TRACEFPS("approximateOrder2!", "recurse{", t);
computeApproximateOrder! x;
computeApproximateOrder! y;
ao := aOrd(x, y);
tchanged? := setApproximateOrder!(t, ao);
TRACEFPS("approximateOrder2!", "recurse}", t);
}
assert(not initialized? t);
if mustInitializeCoefficientStream? then {
TRACEFPS("approximateOrder2!", "set coeff", t);
initializeCoefficientStream!(computeCoefficients, t);
}
TRACEFPS("approximateOrder2!", "}", t);
}
Uses approximateOrderChanged? 245, computeApproximateOrder! 250, Generator 617,
I 47, initializeCoefficientStream! 259b, initialized? 249b, SeriesOrder 289,
setApproximateOrder 260, and TRACEFPS 243.
We have a similar function for operations that just need one argument.
258⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩+
≡ (242) ⊲257 259a ⊳
local approximateOrder!(
computeCoefficients: I -> Generator R,
newOrder: SeriesOrder -> SeriesOrder,
x: %
)(t: %): () == {
TRACEFPS("approximateOrder1!", "{ t", t);
TRACEFPS("approximateOrder1!", "x", x);
initialized? t => {TRACEFPS("approximateOrder1!", "i}", t); return}
ochanged?: Boolean := T.approximateOrderChanged?;
mustInitializeCoefficientStream? := T.approximateOrder = unknown;
macro aOrd x == newOrder(X.approximateOrder);
ao: SeriesOrder := aOrd x;
if ao = unknown then ao := infinity; -- start at maximum
tchanged?: Boolean := setApproximateOrder!(t, ao);
if ochanged? or tchanged? then {
TRACEFPS("approximateOrder1!", "recurse{", t);
computeApproximateOrder! x;
ao := aOrd x;
tchanged? := setApproximateOrder!(t, ao);
TRACEFPS("approximateOrder1!", "recurse}", t);
}
assert(not initialized? t);
if mustInitializeCoefficientStream? then {
TRACEFPS("approximateOrder1!", "set coeff", t);
initializeCoefficientStream!(computeCoefficients, t);
}
TRACEFPS("approximateOrder1!", "}", t);
}
Uses approximateOrderChanged? 245, computeApproximateOrder! 250, Generator 617,
I 47, initializeCoefficientStream! 259b, initialized? 249b, SeriesOrder 289,
setApproximateOrder 260, and TRACEFPS 243.
And finally, we have a version where we assume that the computation of the
approximate order is given by some function that does not involve (through
recursion) the approximat order or t.
259a⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩+
≡ (242) ⊲258 259b ⊳
local approximateOrder!(
computeCoefficients: I -> Generator R,
newOrder: () -> SeriesOrder
)(t: %): () == {
TRACEFPS("approximateOrder0!", "{", t);
initialized? t => {TRACEFPS("approximateOrder0!", "i}", t); return}
assert(T.approximateOrder = unknown);
ao := newOrder();
setApproximateOrder!(t, ao);
initializeCoefficientStream!(computeCoefficients, t);
TRACEFPS("approximateOrder0!", "}", t);
}
Uses Generator 617, I 47, initializeCoefficientStream! 259b, initialized? 249b,
SeriesOrder 289, setApproximateOrder 260, and TRACEFPS 243.
Note that through the following function we only initialize the data structure of
x, but do not actually compute any coefficient in accordance with Convention 2.
The function setApproximateOrder! returns true if the approximate order has
been changed and false otherwise. It sets the approximateOrderChanged? entry in
the representation of its first argument to this return value.
9.2.4 Zero Recognition
There are cases where we can tell whether an infinite series is zero.
- The series is explicitly created as the zero series. Then it is the constant
stream consisting of entries that are all 0 and the order is explicitly set
to infinity.
- The series was computed from other series and after computing the order,
it still is infinity. That happens, for example, if two zero series are added
or a zero series is multiplied by another series.
Note that we fail to recognize, for example, that a sum of an infinite series
and its negation is zero. The function zero? is only a partial zero test.
261⟨implementation: FormalPowerSeries 261⟩≡ (242) 262 ⊳
zero?(x: %): Boolean == {
TRACEFPS("zero?", "{", x);
initialize! x;
TRACEFPS("zero?", "}", x);
X.order = infinity;
}
Uses TRACEFPS 243.
9.2.5 Series Constructors
The simplest way to create a series is by giving an explicit stream s or a generator g.
Since no other information is given, the only reasonable guess is that the
approximate order is zero. See Section 9.2.1 for the fields in the representation.
262⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲261 263b ⊳
coerce(g: Generator R): % == (stream(g) $ DataStream(R)) :: %;
coerce(s: DataStream R): % == BRACKET(
unknown, -- order
0, -- approximateOrder
false, -- approximateOrderChanged?
doNothing, -- computeApproximateOrder!
true, -- initializedCoefficients?
s -- coefficientStream
);
Uses approximateOrderChanged? 245, BRACKET 245, coefficientStream 245,
computeApproximateOrder! 250, DataStream 386, Generator 617,
and initializedCoefficients? 245.
Note that the function initialize! takes care of improving the approximate
order so we do not need to do anything to compute an approximate order. It is for
this reason that here and for the following few cases the function doNothing is the
right choice.
Next let us define the the constant series 0, 1, monom, and term. The order of
those series is known in advance. Thus we can use a special auxiliary function new
to shorten the code. See Section 9.2.1 for the fields in the representation.
263a⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩+
≡ (242) ⊲260 265a ⊳
new(o: SeriesOrder, g: Generator R): % == BRACKET(
o, -- order
o, -- approximateOrder
false, -- approximateOrderChanged?
doNothing, -- computeApproximateOrder!
true, -- initializedCoefficients?
stream g -- coefficientStream
);
Uses approximateOrderChanged? 245, BRACKET 245, coefficientStream 245,
computeApproximateOrder! 250, Generator 617, initializedCoefficients? 245,
and SeriesOrder 289.
263b⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲262 264a ⊳
0: % == SETNAME("0") new(infinity, generate yield 0);
1: % == SETNAME("1") new(0, generate {yield 1; yield 0});
monom: % == SETNAME("x") new(1, generate {yield 0; yield 1; yield 0});
Uses SETNAME 243.
The the implementation of term is only slightly more complicated since we must
check whether it might give the zero series.
The function new is used for recursive definitions in conjunction with set! below.
Both functions are described in FormalPowerSeriesCategory. Actually, it is
completely irrelevant what is put into the data structure, because before any stream
that is created by new is used it must be filled with proper data by using the set!
function.
However, instead of using doNothing, we are a bit more careful to signal an error
if the (uninitialized) stream created by new is accidentially asked to reveal
coefficients.
265a⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩+
≡ (242) ⊲263a 270a ⊳
local uninitialized(x: %): () == {
TRACEFPS("uninitialized", "", x);
never;
}
Uses TRACEFPS 243.
The function set! must always be in accordance with the actual representation,
see Section 9.2.1.
9.2.6 Series Selector Functions
For the ordinary generating series
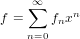 |
(97)
|
coefficient(f, n) returns fn. Note that the function zero? starts a
computation of an approximate order.
ToDo ⊲ 39 ⊳ rhx ⊲ 29 ⊳ 15-Sep-2006: Maybe
f.n should also be allowed.
Note that the computation of the order and the approximate order has
to obey Convention 2. Thus, we can only check the coefficients that have
already been computed. This is taken care of by the function initialize!.
266b⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲266a 267a ⊳
order (x: %): SeriesOrder == {initialize! x; X.order}
approximateOrder(x: %): SeriesOrder == {initialize! x; X.approximateOrder}
Uses SeriesOrder 289.
9.2.7 Creating New Series for Recursive Use
Convention 2 forbids to do any costly computation. In order to prevent computations
from happening, we create a new series by giving appropriate functions as arguments
which encode how the coefficients of the new series are computed. Additionally, we
also require a function that returns an approximate order from the given approximate
order(s).
There is a nullary, univariate and a bivariate version. The univariate
version is used for univariate operations like, for example, differentiate,
integrate, and exponentiate. The bivariate version is invoked for +, *, and
compose. For use of the nullary version see the implementation of coerce in
CycleIndexSeries.
Note that the functions approximateOrder! just forms a function closure, but
does not actually compute any order during the call to one of the following
functions.
The macros NEW1 and NEW2 are only relevant for tracing the computation.
Let us start with the binary version.
268⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲267b 269a ⊳
new(
computeCoefficients: I -> Generator R,
orderOp: (SeriesOrder, SeriesOrder) -> SeriesOrder,
x: %,
y: %
): % == new(approximateOrder!(computeCoefficients, orderOp, x, y));
macro NEW2(op)(computeCoefficients, orderOp, x, y) == {
SETNAME("("+name(x)+op+name(y)+")")
new(computeCoefficients, orderOp, x, y);
}
Defines:
NEW2, used in chunks 270b, 274a, and 278a.
Uses Generator 617, I 47, name 198, SeriesOrder 289, and SETNAME 243.
The unary version is very similar.
269a⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲268 269b ⊳
new(
computeCoefficients: I -> Generator R,
orderOp: SeriesOrder -> SeriesOrder,
x: %
): % == new(approximateOrder!(computeCoefficients, orderOp, x));
macro NEW1(op)(computeCoefficients, orderOp, x) == {
SETNAME(op+"("+name(x)+")")
new(computeCoefficients, orderOp, x);
}
Defines:
NEW1, used in chunks 279b and 281a.
Uses Generator 617, I 47, name 198, SeriesOrder 289, and SETNAME 243.
The nullary version works in a similar fashion, too.
269b⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲269a 270b ⊳
new(
computeCoefficients: I -> Generator R,
orderOp: () -> SeriesOrder
): % == new(approximateOrder!(computeCoefficients, orderOp));
Uses Generator 617, I 47, and SeriesOrder 289.
All three versions above use the following function to build the data structure.
270a⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩+
≡ (242) ⊲265a 271a ⊳
-- This function is, in fact, a local one, but the compiler forbids to
-- put a "local" keyword in front.
new(approximatOrder!: % -> ()): % == BRACKET(
unknown, -- order
unknown, -- approximateOrder
true, -- approximateOrderChanged?
approximatOrder!, -- computeApproximateOrder!
false, -- initializedCoefficients?
uninitialized -- coefficientStream
);
Uses approximateOrderChanged? 245, BRACKET 245, coefficientStream 245,
computeApproximateOrder! 250, and initializedCoefficients? 245.
9.2.8 Series Addition
According to the example code given in Section 9.2, we must be very careful while
adding two series. With a series definition of the form s = x + s2, the computation of
a coefficient should only be done if the memory has been reserved for the data
structure. Similarly, the computation of an approximate order has to be delayed until
all the data structures (of the series that are involved) are created. For this
reason the addition operation of series cannot check for zero of one of its
arguments at creation time, since zero? starts a computation of an approximate
order.
The last two arguments of new give a way to compute the coefficients of x + y and
an approximate order from the orders of x and y.
270b⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲269b 272 ⊳
(x: %) + (y: %): % == NEW2("+")(plus(x, y), min, x, y);
Uses NEW2 268.
Generating the coefficients of a sum of two series is a simple task. The third
parameter give a lower approximation on the order of the series.
271a⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩+
≡ (242) ⊲270a 274b ⊳
local plus(x: %, y: %)(aord: I): Generator R == generate {
TRACE("Series + ", aord);
for n: I in 1..aord repeat yield 0@R;
for n: I in aord.. repeat yield coefficient(x, n) + coefficient(y, n);
}
Uses Generator 617 and I 47.
The following code takes eventually constant streams into account. In other
words, for series with finite support we do not produce much overhead.
ToDo ⊲ 41
⊳ rhx ⊲ 31 ⊳ 19-Sep-2006: Carefully test the following code chunk. In particular it
should take care of the
approximate order.
16-Feb-2007: The following code is now quite old, since we have refactored the
generator stuff to the one above.
271b⟨NOTYET: implementation: FormalPowerSeries 271b⟩≡
local (x: %) + (y: %): Generator R == generate {
TRACE("Series ", "+");
cx := x :: DataStream R; cy := y :: DataStream R;
gx: Generator R := elements cx; gy: Generator R := elements cy;
nx: R := 0; ny: R := 0;
for ix in gx for iy in gy repeat {
(nx, ny) := (ix, iy);
yield (nx+ny);
}
-- At least one of the following loops is empty.
for ix in gx repeat {nx := ix; yield (nx+ny)} -- might be empty
for iy in gy repeat yield (nx+iy); -- might be empty
}
Uses DataStream 386 and Generator 617.
9.2.9 Finite Sum
ToDo ⊲ 42 ⊳ rhx ⊲ 32 ⊳ 15-Feb-2007: The following code does not take into
account if each of the finitely many series is finite. The result should be a finite series,
but is currently not.
rhx ⊲ 33 ⊳ 16-Feb-2007: Both of the following
sum functions should
not be used in
recursive definitions of series.
272⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲270b 273a ⊳
local sumCoefficients(a: Array %): Generator R == generate {
last: I := #a-1;
assert(last>=0);
for n: I in 0.. repeat {
r: R := coefficient(a.0, n);
for i in 1..last repeat r := r + coefficient(a.i, n);
yield r;
}
}
sum(a: Array %): % == {
#if TRACE
names: String := "sum("+name a.0;
for i in 1..#a-1 repeat {
names := names + ","+name a.i;
}
names := names + ")";
SETNAME(names)((sumCoefficients a) :: %);
#else
(sumCoefficients a) :: %;
#endif
}
Uses Array 599, Generator 617, I 47, name 198, SETNAME 243, and String 65.
9.2.10 Potentially Infinite Sum
ToDo ⊲ 43 ⊳ rhx ⊲ 34 ⊳ 31-Jan-2007: The following code does not take into
account if the given sequence of series is finite and at the same time each of the finite
series is finite. The result should be a finite series, but is currently not.
In the following code we first access the n-th coefficient of the n-th given series
(n = 0,1,2,…). Only after this access, the value m := #s − 1 gives the index of the
last series that has to be taken into account no matter whether the sequence s is
finite or infinite. Now since DataStream repeats the last element of the stream if the
stream is finite, r = (sm)n. So we only need to add the remaining values for the
indicies i = 0,1,…,m − 1.
273b⟨implementation: FormalPowerSeries sum generator 273b⟩≡ (273a)
for n: I in 0.. repeat {
r: R := coefficient(s.n, n); -- compute [x^n] s(n).
for i in 0..#s-2 repeat r := r + coefficient(s.i, n);
yield r;
}
Uses I 47.
9.2.11 Series Multiplication
A similar argument about full lazyness as given in Section 9.2.8 also applies
here.
Multiplication of formal power series is explained at the API description of *.
274a⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲273a 275b ⊳
(x: %) * (y: %): % == NEW2("*")(times(x, y), +, x, y);
Uses NEW2 268.
ToDo ⊲ 44 ⊳ rhx ⊲ 35 ⊳ 24-Aug-2006: Note that the underlying streams might
be constant from some point on. Currently, we don’t take this into account.
274b⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩+
≡ (242) ⊲271a 278b ⊳
local times(x: %, y: %)(aord: I): Generator R == generate {
TRACE("Series *: ", aord);
for n: I in 1..aord repeat yield 0@R;
for n: I in aord.. repeat yield {⟨n-th coefficient of x ⋅ y 275a⟩}
}
Uses Generator 617 and I 47.
In the following code we take care of the current approximate order of x and y in
order not to compute too much.
275a⟨n-th coefficient of x ⋅ y 275a⟩≡ (274b)
nthCoefficient: R := 0;
low: I := (X.approximateOrder) :: I;
high: I := n - (Y.approximateOrder) :: I;
for k in low..high | not zero?(cx:=coefficient(x,k)) repeat {
nthCoefficient := nthCoefficient + cx * coefficient(y, n-k);
}
nthCoefficient;
Uses I 47.
9.2.12 Potentially Infinite Products
In this section we implement potentially infinite products. In order to be able to do
this we put some restrictions on the (possibly infinite) input series. Let g1,g2,g3,… be
the series generated by the input generator g. For every n the series gn must be of
the form
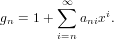 |
(98)
|
Given that restriction, we can compute the n-th coefficient of the (infinite)
product by just multiplying the first n series.
The last line in the following code takes care of the case that g only generates
finitely many elements.
276⟨implementation: FormalPowerSeries product generator 276⟩≡ (275b)
for i in 0..0 for x in g repeat z := x;
yield coefficient(z, 0);
yield coefficient(z, 1);
n: I := 2;
for x in g repeat {
z := z * x;
yield coefficient(z, n);
n := next n;
}
for c in elements(z :: DataStream R, n) repeat yield c;
Uses DataStream 386 and I 47.
9.2.13 Series Composition
In order to compute f(g(x)) for two series f and g, we use a simple formula.
Assume that
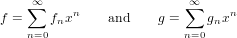 |
(99)
|
then, if we substitute g into f, we get 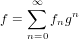 |
(100)
|
In order to use the stream nature of f and g, we rather compute f(g) in the
following way.
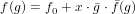 |
(101)
|
where f = f0 + x ⋅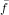 and g = g0 + x ⋅
and g = g0 + x ⋅ . Note that we require g0 = 0 and thus
the recursion formula simplifies to
. Note that we require g0 = 0 and thus
the recursion formula simplifies to 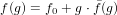 |
(102)
|
ToDo ⊲ 45 ⊳ rhx ⊲ 36 ⊳ 02-Oct-2006: Should reconsider the following
implementation in order to take care of the case when
x is a series whose constant
term is zero and at the same time
y = 0. In that case the order should become
infinity.
See also ToDo 55 (compose).
278a⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲275b 279a ⊳
compose(x: %, y: %): % == NEW2(" o ")(compose(x, y), *, x, y);
Uses NEW2 268.
ToDo ⊲ 46 ⊳
rhx ⊲ 38 ⊳ 03-Oct-2006: If possible allow a
rest function on streams that uses only
constant time. We could do it if the
FormalPowerSeries representation stores the
starting index.
rhx ⊲ 39 ⊳ 26-Feb-2007: Maybe we should have a function
-
-
compose: (x: Generator R, y: %) -> %
in order to avoid reserving memory for
restX.
278b⟨implementation: FormalPowerSeries: auxiliary functions 249a⟩+
≡ (242) ⊲274b
local compose(x: %, y: %)(aord: I): Generator R == generate {
TRACE("Series compose ", aord);
assert(zero? coefficient(y, 0));
yield coefficient(x, 0);
restX: % := SETNAME("R("+name(x)+")")(elements(x::DataStream R, 1)::%);
z: % := compose(restX, y) * y;
zero? z => 0@R; -- initialize z!!!
d: DataStream R := z :: DataStream R;
for e in elements(d, 1) repeat yield e;
}
Uses DataStream 386, Generator 617, I 47, name 198, and SETNAME 243.
9.2.14 Series Differentiation
We implement the function differentiate, which can only be done if the coefficient
domain provides appropriate functionality. It basically means, that the coefficient
ring R is a ℤ-algebra.
279a⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲278a 280b ⊳
if R has with {*: (Integer, %) -> %} then {
⟨implementation: FormalPowerSeries differentiate 279b⟩
}
Uses Integer 66.
279b⟨implementation: FormalPowerSeries differentiate 279b⟩≡ (279a) 280a ⊳
differentiate(x: %): % == NEW1("D")(differentiate x, boundedDecrement, x);
Uses NEW1 269a.
Note that in the code below n[xn]x corresponds to the coefficient of xn−1 in x.
ToDo ⊲ 47 ⊳ mrx ⊲ 6 ⊳ 11-Feb-2007: I think it would make sense to use names
for variables that indicate the object they refer to, when possible. For
example
- x, y, z for formal variables,
- r, s, t or X, Y , Z for series…
280a⟨implementation: FormalPowerSeries differentiate 279b⟩+
≡ (279a) ⊲279b
local differentiate(x: %)(aord: I): Generator R == generate {
import from Z;
TRACE("Series differentiate ", aord);
for n: I in 1..aord repeat yield 0@R;
for n: I in next aord .. repeat yield (n::Z) * coefficient(x, n);
}
Uses Generator 617, I 47, and Z 47.
9.2.15 Series Integration
We implement the function integrate, which can only be done if the coefficient
domain provides appropriate functionality. It basically means, that the coefficient
ring R is a ℚ-algebra.
280b⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲279a 282 ⊳
if R has with {*: (Fraction Integer, %) -> %} then {
⟨implementation: FormalPowerSeries integrate 281a⟩
}
Uses Integer 66.
281a⟨implementation: FormalPowerSeries integrate 281a⟩≡ (280b) 281b ⊳
integrate(x: %, integrationConstant: R == 0): % == {
zero? integrationConstant => NEW1("I")(integrate x, increment, x);
SETNAME("I1("+name(x)+")") new(0, integrateNonZero(x, integrationConstant));
}
Uses I 47, name 198, NEW1 269a, and SETNAME 243.
281b⟨implementation: FormalPowerSeries integrate 281a⟩+
≡ (280b) ⊲281a
local integrate(x: %)(aord: I): Generator R == generate {
import from Z, Q;
TRACEFPS("Series integrate", "", x);
TRACE("Series integrate ", aord);
for n: I in 1..aord repeat yield 0@R;
for n: I in aord .. repeat yield inv(n::Z) * coefficient(x, prev n);
}
local integrateNonZero(x: %, integrationConstant: R): Generator R == generate {
import from Z, Q;
TRACEFPS("Series integrate const", "", x);
yield integrationConstant;
aox: SeriesOrder := approximateOrder x;
assert(aox ~= unknown);
TRACE("Series integrate aox=", aox);
aox = infinity => yield 0@R;
i: I := aox :: I;
for n: I in 1..i repeat yield 0@R;
for n: I in next i .. repeat yield inv(n::Z) * coefficient(x, prev n);
}
Uses Generator 617, I 47, Q 47, SeriesOrder 289, TRACEFPS 243, and Z 47.
9.2.16 Series Exponentiation
We implement the function exponentiate, which can only be done if the coefficient
domain provides appropriate functionality. It basically means, that the coefficient
ring R is a ℚ-algebra.
Our implementation uses the recursion formula
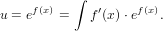 |
(103)
|
Note that the computation of exp(f) for a power series f can only be done, if
f = ∑
n=1∞fnxn, i. e., the constant of the series is zero.
282⟨implementation: FormalPowerSeries 261⟩+
≡ (242) ⊲280b
if R has with {*: (Integer, %) -> %; *: (Fraction Integer, %) -> %} then {
⟨implementation: FormalPowerSeries exponentiate 283⟩
}
Uses Integer 66.
ToDo ⊲ 48 ⊳ rhx ⊲ 40 ⊳ 02-Feb-2007: We should actually assert that the
zeroth coefficient of
x is zero, but adding and executing
assert(zero? coefficient(x, 0));
|
would violate our Convention 2 that series computation must be fully lazy.
(I think I must extend that Convention to actual state lazyness not only for the order
computation but in general.)
283⟨implementation: FormalPowerSeries exponentiate 283⟩≡ (282)
exponentiate(x: %): % == {
s: % := new();
set!(s, integrate(differentiate x * s, 1));
SETNAME("EXP("+name(x)+")")(s);
}
Uses name 198 and SETNAME 243.
It follows an alternative of exponentiate which uses less memory since the
intermediate allocation of DataStream for differentiate and * are avoided.
However, this version runs slower and is therefore not used. It is recoreded here in
order to show what has already been tested.
The implementation builds on Proposition 5.1.7 of [Sta99], but the formula is
translated for use with formal power series that are not exponential series.
In order to compute for a power series f = ∑
n=1∞fnxn a power series
h = ∑
n=0∞hnxn a power series such that h = exp(f) one can use the following
recursion.
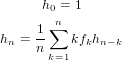 |
(104)
(105)
|
We decided against the following implementation since the implementation above
immediately benefits from an implementation of relaxed multiplication of power
series according to [vdH02].
In the following code we take care of the current approximate order of f in order
not to compute too much.
284⟨UNUSED and slower: n-th coefficient of h = exp(f) 284⟩≡
import from Z, Q;
nthCoefficient: R := 0;
low: I := (rep(f).approximateOrder) :: I;
for k in low..n | not zero?(cf:=coefficient(f,k)) repeat {
nthCoefficient := nthCoefficient + (k::Z) * coefficient(h, n-k) * cf;
}
inv(n::Z) * nthCoefficient;
Uses I 47, Q 47, and Z 47.
285a⟨UNUSED and slower implementation: FormalPowerSeries exponentiate 285a⟩≡ 285b ⊳
local exponentiate(f: %, h: %): Generator R == generate {
assert(zero? coefficient(f, 0));
yield 1;
for n: I in 1.. repeat yield {⟨n-th coefficient of h = exp(f) (never defined)⟩}
}
Uses Generator 617 and I 47.
285b⟨UNUSED and slower implementation: FormalPowerSeries exponentiate 285a⟩+
≡ ⊲285a
exponentiate(f: %): % == {
h: % := new();
set!(h, exponentiate(f, h) :: %);
SETNAME("EXP("+name(f)+")")(h);
}
Uses name 198 and SETNAME 243.
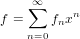
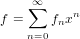

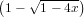 = x + x2 + 2x3 + 5x4 + 14x5 + O(x6)
= x + x2 + 2x3 + 5x4 + 14x5 + O(x6)
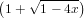 = 1 − x − x2 − 2x3 − 5x4 − 14x5 + O(x6)
= 1 − x − x2 − 2x3 − 5x4 − 14x5 + O(x6)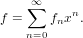
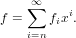
 not initialized? t
not initialized? t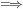 T.order = unknown
T.order = unknown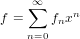
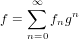
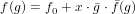
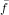 and g = g0 + x ⋅
and g = g0 + x ⋅ . Note that we require g0 = 0 and thus
the recursion formula simplifies to
. Note that we require g0 = 0 and thus
the recursion formula simplifies to