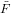 (x)
(x)
The cycle index series ZF(x1,x2,…) of a combinatorial species F is a formal power series in infinitely many variables that incorporates many properties of the species. In particular, specialization of the cycle index series gives the exponential and the ordinary generating series of a species.
| F(x) | = ZF(x,0,0,…) | (128) |
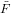 (x) (x) | = ZF(x,x2,x3,…) | (129) |
Definition 10.5. [BLL98, Def. 1.2.6] The cycle index series of a species of structures F is the formal power series (in an infinite number of variables x1,x2,x3,…)
![( )
∑ 1-∑ σ1 σ2 σn
ZF (x1,x2,x3,...) = n! fixF [σ]x1 x2 ...x n ,
n≥0 σ∈Sn](combinat234x.png) | (130) |
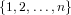 , n ∈ ℕ,
and
, n ∈ ℕ,
and
| FixF[σ] | = ![{s ∈ F [n]|F[σ](s) = s }](combinat236x.png) | (131) |
| fixF[σ] | = card(FixF[σ]) = (F[σ])1, | (132) |
The cycle type ((F[σ])1,(F[σ])2,…) of F[σ] only depends on the cycle type
(σ1,…,σn) of the permutation σ. Two permutations σ and τ have the same cycle type
if and only if there exists a permutation π such that σ = π−1τπ. Functoriality of F
gives F[σ] = F[π]−1F[τ]F[π] and proves the above statement. Thus, for
j = (j1,…,jn) with j1 + 2j2 +  + njn = n we can define fixF[j] as fixF[σ] for any
permutation σ ∈ Sn with cycle type j.
+ njn = n we can define fixF[j] as fixF[σ] for any
permutation σ ∈ Sn with cycle type j.
Since there are 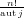 permutations of cycle type j we can rewrite (130)
into
permutations of cycle type j we can rewrite (130)
into
| ZF(x1,x2,x3,…) | = ∑
n≥0 ∑
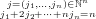 fixF[j] fixF[j]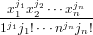 | (133) |
= ∑
n≥0 ∑
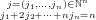 fixF[j] fixF[j]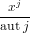 | (134) |
Definition 10.6. [BLL98, App. 1, Def. 1] An action of a (multiplicative) group G on an A-weighted set (Y,w) is a function
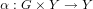 | (135) |
Definition 10.7. [Ker91, p. 71] Let α : G × Y → Y be an action of a (finite) group G on a finite set Y with n = card(Y ). The cycle index polynomial C(G,Y ;x1,…,xn) ∈ ℚ[x1,…,xn] is defined by
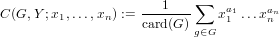 | (136) |
 = φ(g) and
.
= φ(g) and
.
Contrary to what one might think, the cycle index series is not the formal sum of the cycle index polynomial of the actions
![αn : Sn × F [n ] → F[n], (σ,s) ↦→ αn(σ,s) = σ⋅F (s) = F[σ](s).](combinat246x.png) | (137) |
![∑
ZF(x1,x2,...) ⁄= C (Sn,F[n];x1,x2,...,xn).
n≥0](combinat247x.png) |
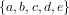 , a set of 5 elements and the permutation σ = (ab)(cde), the
permutation F[σ] contains cycles of length 6. That is clearly in contradiction to the
number of variables used inside the parentheses in (130) for n = 5.
, a set of 5 elements and the permutation σ = (ab)(cde), the
permutation F[σ] contains cycles of length 6. That is clearly in contradiction to the
number of variables used inside the parentheses in (130) for n = 5.
The cycle index series is rather the formal sum (over all isomorphism types 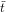 of
F) of the cycle index polynomial of the actions
of
F) of the cycle index polynomial of the actions
![αt : Gt × [n] → [n], (σ,s) ↦→ αt(σ,s) = α(σ,s) = σ(s),](combinat250x.png) | (138) |
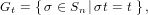 | (139) |
 ∈ F[U] ∕ ∼ (see
Proposition 4.3.2 in [BLL98]).
∈ F[U] ∕ ∼ (see
Proposition 4.3.2 in [BLL98]).
Note that according to Definition 10.2, 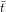 denotes the isomorphism type
denotes the isomorphism type
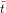 = Sn(t) ∈ T(Fn) of an element t ∈ F[n].
= Sn(t) ∈ T(Fn) of an element t ∈ F[n].
Similar to [BLL98, Prop. 4.3.2] we have
| ZF(x1,x2,…) | = ∑
n≥0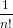 ∑
σ∈Sn fixF[σ]x1σ1
…xnσn ∑
σ∈Sn fixF[σ]x1σ1
…xnσn
| ||
= ∑
n≥0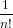 ∑
σ∈Sn card( ∑
σ∈Sn card(![{s ∈ F [n]|F[σ](s) = s }](combinat257x.png) )x1σ1
…xnσn )x1σ1
…xnσn
| |||
= ∑
n≥0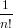 ∑
σ∈Sn ∑
s∈F[n][F[σ](s) = s]x1σ1
…xnσn ∑
σ∈Sn ∑
s∈F[n][F[σ](s) = s]x1σ1
…xnσn
| |||
= ∑
n≥0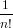 ∑
s∈F[n] ∑
σ∈Sn[F[σ](s) = s]x1σ1
…xnσn ∑
s∈F[n] ∑
σ∈Sn[F[σ](s) = s]x1σ1
…xnσn
| |||
= ∑
n≥0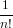 ∑
s∈F[n] ∑
σ∈(Sn)sx1σ1
…xnσn ∑
s∈F[n] ∑
σ∈(Sn)sx1σ1
…xnσn
| |||
= ∑
n≥0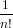 ∑ ∑
 ∈T(Fn) card(Sn(t))∑
σ∈(Sn)tx1σ1
…xnσn ∈T(Fn) card(Sn(t))∑
σ∈(Sn)tx1σ1
…xnσn
| |||
= ∑
n≥0 ∑
t∈T(Fn)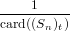 ∑
σ∈(Sn)tx1σ1
…xnσn ∑
σ∈(Sn)tx1σ1
…xnσn
| |||
= ∑
n≥0 ∑
 ∈T(Fn)C(Gt,[n];x1,…,xn). ∈T(Fn)C(Gt,[n];x1,…,xn). |
![{
1 if P (s) is true,
[P (s)] =
0 otherwise.](combinat265x.png) | (140) |
In the above derivation we relied on the Cauchy-Frobenius Theorem.
Theorem 10.8 (Cauchy-Frobenius). Let G be a finite group acting on a finite set Y then the number of orbits is the average over the number of fixed points, i.e.,
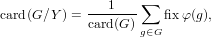 | (141) |
The main idea for the implementation of cycle index series is that it is modelled by a univariate formal power series (in x) of polynomials in infinitely many variables x1,x2,… The variable x will, of course, never be considered for anything else than grouping the infinitely many power products into homogeneous polynomials of (weighted) degree n. In fact, we use equation (134).
We start by introducing a variable domain that models x1,x2,… together with a weight function. Each variable xi is given the weight i. The weight is extended to powers of variables by defining the weight of xie to be i⋅e. And the weight of a power product to be the sum of the weights of the variables (counted with multiplicity) contained in it.
Description
Implements variables x1,x2,…
This domain implements infinitely many variables indexed by positive integers where the weight of each variable is given by its index.
Description
Cycle index series.
CycleIndexSeries is the domain that represents cycle index series, i. e., formal power series in infinitely many variables x1,x2,x3,… of the form
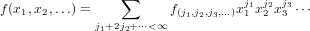 | (142) |
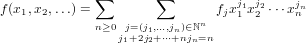 | (143) |
In fact, if f = ZF for some combinatorial species F then fj = ![fixF-[j]
autj](combinat269x.png) where aut(j) is
defined by (145).
where aut(j) is
defined by (145).
If we denote by ℕ(ℕ) the set of finite sequences of natural numbers then a cycle index series f is a function from ℕ(ℕ) to ℚ in analogy to the fact that a formal power series (over ℚ) is a function from ℕ to ℚ.
Exports of CycleIndexSeries
coefficient: (%, T) -> Fraction Integer Coefficient of a given cycle type.
aut: T -> Integer A factor for the number of permutations of a givencycle type.
count: (%, T) -> Integer Counts the number of structures corresponding to a certain cycle type.
stretch: (%, MachineInteger) -> % Stretch a cycle index series.
compose: (%, %) -> % Composition or plethystic substitution of two cycle index series.
functorialCompose: (%, %) -> % Functorial composition of two cycle index series.
coerce: % -> OrdinaryGeneratingSeries Extract the type generating series from the cycle index series.
coerce: % -> ExponentialGeneratingSeries Extract the exponential generating series from the cycle index series.
Export of CycleIndexSeries
coefficient: (%, T) -> Fraction Integer
Usage
macro {
V == CycleIndexVariable;
T == SparseIndexedPowerProduct(V, MachineInteger);
}
import from V, T;
s: CycleIndexSeries := ...
t: T := power(3::V,2) * power(5::V,3) * power(6::V,1);
q: Q := coefficient t;
Description
Coefficient of a given cycle type.
If for a combinatorial species F
![Z = ∑ ∑ fix F[j] xj
F n≥0 j=(j ,...,j )∈ℕn autj
j1+2j12+⋅⋅⋅+nnjn=n](combinat270x.png) | (144) |
![fixaFut[jj]](combinat271x.png) .
.
Export of CycleIndexSeries
aut: T -> Integer
Usage
macro {
V == CycleIndexVariable;
T == SparseIndexedPowerProduct(V, MachineInteger);
}
import from V, T;
t: T := power(3::V,2) * power(5::V,3) * power(6::V,1);
z: Z := aut t;
Description
A factor for the number of permutations of a givencycle type.
Given a cycle type j = (j1,j2,…,jn) such that j1 + 2j2 +  + njn = n. Then
+ njn = n. Then
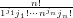 gives the number of permutations having cycle type k. We define
gives the number of permutations having cycle type k. We define
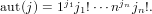 | (145) |
Export of CycleIndexSeries
count: (%, T) -> Integer
Usage
macro {
V == CycleIndexVariable;
T == SparseIndexedPowerProduct(V, MachineInteger);
}
import from V, T;
t: T := power(3::V,2) * power(5::V,3) * power(6::V,1);
z: Z := count t;
Description
Counts the number of structures corresponding to a certain cycle type.
If for a combinatorial species F
![Z = ∑ ∑ fix F[j] xj
F n≥0 j=(j ,...,j )∈ℕn autj
j1+2j12+⋅⋅⋅+nnjn=n](combinat275x.png) | (146) |
Export of CycleIndexSeries
stretch: (%, MachineInteger) -> %
Usage
x: CycleIndexSeries := cycleIndexSeries$SetSpecies(Integer);
k: MachineInteger := 3;
s: CycleIndexSeries := stretch(x, k);
Description
Stretch a cycle index series.
For some integer k and a given cycle index series
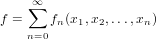 |
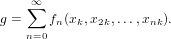 |
Remarks
This functions respects the fact that coefficient(g,n) returns a polynomial of (weighted) degree n, i. e., the function coefficients(g) returns a sequence with gaps of size k − 1 between actual non-zero polynomials.
Let us start with some simple auxiliary functions which stretch power products and polynomials.
We keep those functions here since we see no reason why they should live in SparseIndexedPowerProduct or SparseDistributedPolynomial, since those domains are general purpose domains.
Export of CycleIndexSeries
compose: (%, %) -> %
Usage
x: CycleIndexSeries := cycleIndexSeries$SetSpecies(Integer);
y: CycleIndexSeries := cycleIndexSeries$NonEmpty(SetSpecies)(Integer);
z: CycleIndexSeries := compose(x, y);
Description
Composition or plethystic substitution of two cycle index series.
Let f and g be two cycle index series with g(0,0,…) = 0 and let for gk denote the series given by
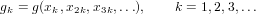 |
This implementation overrides the implementation of compose that is inherited by CycleIndexSeries from FormalPowerSeries.
Let us abbreviate stretch(f,k) by fk. Our implementation relies on the fact that for two series f and g we have
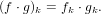 | (147) |
| f | = ∑
n≥0 ∑
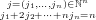 fj ⋅ x1j1
⋅ x2j2 fj ⋅ x1j1
⋅ x2j2
 xnjn xnjn
|
| f ∘ g | = ∑
n≥0 ∑
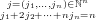 fj ⋅ (g1)j1
⋅ (g2)j2 fj ⋅ (g1)j1
⋅ (g2)j2
 (gn)jn (gn)jn
| (148) |
= ∑
n≥0 ∑
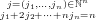 fj ⋅ (gj1
)1 ⋅ (gj2
)2 fj ⋅ (gj1
)1 ⋅ (gj2
)2 (gjn
)n (gjn
)n | (149) |
So let us first give an auxiliary function that computes all the powers of a given series.
First of all we use the same definition as for compose from FormalPowerSeries in order to obey Convention 2. However, the first parameter is a function that is given below and quite different from the corresponding function in FormalPowerSeries.
The following function generates all (homogeneous) polynomials pn that appear as the summands of the outermost sum of (149). Note that a variables xi has weight i and that we take this weight into account if we speak of homogeneous polynomials.
When this function is called the third parameter gives a good guess for the resulting order of the series.
As given above we sum over all n ∈ ℕ. For each such n there is only a polynomial with finitely many power products to consider.
Plethystic substitution of a polynomial p of (weighted) degree n with a power series g is done by adding all the finitely many series coming from the substitution of g into the terms of p.
We are left with the problem of plethystic substitution of a series g into a coefficient-power product pair. According to powers, the second parameter can be seen as (g,g2,g3,…). Note, however, that the first index of a DataStream is 0.
As stated in equation (147) above, we rely on the property that stretching commutes with multiplication.
Export of CycleIndexSeries
functorialCompose: (%, %) -> %
Description
Functorial composition of two cycle index series.
Let F, G, and H be species such that H = F ⊓ ⊔ G. The cycle index series ZH = ZF ⊓ ⊔ ZG of H is defined as
| ZH | = ∑
n=0∞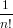 ∑
σ∈Sn fixF[(G[σ])1,(G[σ])2,…,(G[σ])lj]xσ ∑
σ∈Sn fixF[(G[σ])1,(G[σ])2,…,(G[σ])lj]xσ | (150) |
= ∑
n≥0 ∑
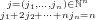 fixF[(G[j])1,(G[j])2,…,(G[j])lj] fixF[(G[j])1,(G[j])2,…,(G[j])lj]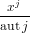 . . | (151) |
Let us implement formula (151) almost literally and deal with the details later.
Looking at the definition of count(f,t), we see that for some cycle type i encoded by t = xi it returns fixF[i]. However, according to formula (151) i = ((G[j])1,(G[j])2,…,(G[j])lj) for some cycle type s = xj.
Let us first deal with the problem of the generation of all cycle types of size n. It clearly corresponds to all partitions j of the integer n. We encode such a partition by a power product s = xj = x1j1…xnjn and generate them via the function cycleTypes.
The generation of integer partitions is relatively simple. One just has to understand that a partition of n can start with a highest part m and the rest is an integer partition of n − m that does not involve parts that are bigger than m (a bound).
Definition 10.9. An integer partition of n ∈ ℕ is tuple j = (j1,j2,…,jn) such that n = ∑ k=1nk ⋅ jk.
An integer partition can be used to denote the cycle type of a permutation σ ∈ Sn.
Definition 10.10. A cycle type of a permutation σ ∈ Sn is a tuple j = (j1,j2,…,jn) where jk denotes the number of cycles of length k in the disjoint cycle decomposition of σ.
We usually encode a cycle type j by a power product of the form
xj = x1j1x2j2 xnjn.
xnjn.
Next we deal with the problem of computing ((G[j])1,(G[j])2,…,(G[j])lj) for some cycle type j that is encoded by s = xj. The function call cycleType(g,s) does this computation.
For the implementation of f ⊓ ⊔ g let us look at equation (151) more closely. We first have to figure out what lj is. Unfortunately, we cannot give a general formula for lj, since it inherently depends on the species G. An upper bound for lj is perfectly fine here, since we only need a finite value in order to stop the computation. Of course, lj ≤ cardG[n], if j = (j1,…,jn) ∈ ℕn, but cardG[n] is much too pessimistic in general. This bound is, however, quite reasonable for some species, like, for example, the species E of sets. Then cardE[n] = 1.
Let σ ∈ Sn be a permutation with cylce type j. If 1 ≤ k ≤ n, jk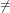 0 and σ is
applied k times to a structure w ∈ G[n] then it is ensured that all labels in w
corresponding to k-cycles in σ are back in place. The same holds if σ is applied
rk times (r ∈ ℕ). Therefore it is clear that σm ⋅ w = (G[σ])m(w) = w if
0 and σ is
applied k times to a structure w ∈ G[n] then it is ensured that all labels in w
corresponding to k-cycles in σ are back in place. The same holds if σ is applied
rk times (r ∈ ℕ). Therefore it is clear that σm ⋅ w = (G[σ])m(w) = w if
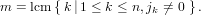 | (152) |
Although the above definition of m just depends on n and j, for an upper bound for lj it makes only sense if it is known that in the functorial composition f ⊓ ⊔ g the series g is equal to a cycle index series ZG of some combinatorial species G. We can therefore compute lj as the minimum
![l= min (cardG [n],lcm {k |1 ≤ k ≤ n,j ⁄= 0 }).
j k](combinat292x.png) | (153) |
We code the above equation into the following function where g stands for ZG and s = xj encodes the cycle index j of some permutation σ ∈ Sn.
The cardinality of G[n] is encoded in the generating series G(x) of G which we do not have available here. However, since we assume g = ZG, we can easily extract that number from the cycle index series similar to the computation of the generating series via the function coerce.
The numbers (G[j])k that are needed in the computation of (151) can be computed using Proposition 2.2.3 of [BLL98]. For completeness, we repeat this proposition here.
Proposition 10.11. Let G be a species of structures, σ ∈ Sn, and k ≥ 1. Then the number of cycles of length k in G[σ] is given by
![( )
(G [σ]) = 1-∑ μ k- fixG[σd],
k k d|k d](combinat293x.png) | (154) |
For the particular case n = 0 there, we conclude that
![{
(G[σ])k = cardG [0], if k = 1, and
0, for k > 1.](combinat294x.png) | (155) |
Note that that the cycle type i of G[σ] only depends on the cycle type j of σ.
The following function computes i = ((G[j])1,(G[j])2,…,(G[j])lj) and encodes it as a power product
![(G[j]) (G[j]) (G[j])l
t = xi = x1 1x 2 2...xlj j.](combinat295x.png) | (156) |
In the following implementation we exchange the roles of d and  in the summand
of (154).
in the summand
of (154).
The only missing part is the cycle type of σk for some permutation σ ∈ Sn with cycle type j.
According to Exercise 2.2.2 in [BLL98] we have
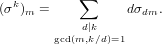 | (157) |
In the above code we use two auxiliary functions. The first one returns true if and only if gcd(i,k) = 1.
The second function simply multiplies all the prime powers contained in k.
Export of CycleIndexSeries
coerce: % -> OrdinaryGeneratingSeries
Description
Extract the type generating series from the cycle index series.
According to Theorem 8 in [BLL98], we have for a species F
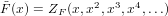 | (158) |
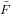 (x) given the cycle index series ZF of the
species.
(x) given the cycle index series ZF of the
species.
According to (158) we basically have to replace all variables xi by xi. We have grouped the cycle index series into homogeneous polynomials pn. The substitution (158) and extraction of the coefficient of xn amounts to summing the coefficients of all power products of the polynomial pn.
Export of CycleIndexSeries
coerce: % -> ExponentialGeneratingSeries
Description
Extract the exponential generating series from the cycle index series.
According to Theorem 8 in [BLL98], we have for a species F
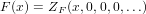 | (159) |
According to (159) we only need to extract the term that solely involves the
variable x1. We have grouped the cycle index series into homogeneous polynomials
pn. The order on the terms (type T) that we have imposed on in type P is such that
it suffices to take the leading coefficient of the pn as long as it is not zero. If pn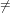 0
then it must contain the power product x1n, since its coefficient corresponds to the
number of structures of size n. We simply extract that coefficient and form a new
series.
0
then it must contain the power product x1n, since its coefficient corresponds to the
number of structures of size n. We simply extract that coefficient and form a new
series.
coefficient(cycleIndexSeries()$Partition ACINT, 4)
Looking in PrimitiveArray(FormalPowerSeries( SparseDistributedPolynomial( ACFraction(ACInteger()), CycleIndexVariable(), SparseIndexedPowerProduct(CycleIndexVariable(), ACMachineInteger())))) for new with code 937065024 >> System error: FOAM-USER::|fiRaiseException| is invalid as a function. |