8.11 Product of Species
Definition 8.10. [BLL98, chp. 1.3] Let F and G be two species of structures. The
species F ⋅ G (also denoted FG), called the product of F and G, is defined as
![(F ⋅G )[U] = ∑ F[U ]× G [U ]
(U ,U ) 1 2
1 2](combinat103x.png) |
(37)
|
where the sum is taken over all pairs (
U1,U2) for which
U =
U1 ∪ U2 and
U1 ∩ U2 =
∅.
The transport along a bijection σ : U → V is carried out by setting, for each
(F ⋅ G)-structure s = (f,g) on U,
 = (F[σ1](f),G[σ2](g))](combinat104x.png) |
(38)
|
where
σi =
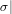 Ui
Ui is the restriction of
σ on
Ui,
i = 1
,2.
Definition 8.11. The cardinality species N is the species of structures defined by
![N[U] = {cardU }](combinat106x.png) |
(39)
|
for any finite set
U and
 = n](combinat107x.png) |
(40)
|
for any bijection
σ :
U → V and
n = card
U = card
V an
N-structure on
U.
Proof. Define the mapping ν : E → N for any finite set U by
![νU : E [U ] → N [U], U ↦→ card U.](combinat108x.png) |
(41)
|
Then for any bijection
σ :
U → V between two finite sets
U and
V of cardinality
n it holds
) = νV(V) = cardV = n](combinat109x.png) |
(42)
|
and
) = N [σ ](n) = n](combinat110x.png) |
(43)
|
Furthermore,
ν has an inverse given by
![μ : N[U] → E[U], cardU ↦→ U.
U](combinat111x.png) |
(44)
|
Therefore
ν is a natural isomorphism from
E to
N. __
There exists exactly one structure for every input set U, so N(x) = E(x) = ex.
Clearly, N ⋅ N has an exponential generating series e2x. Look at (37) to understand
that the sum symbol must be interpreted as a disjoint union.
Let us for a while assume the above sum in (37) is an ordinary (non-disjoint)
union. Then
(N ⋅ N)[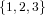 ] ] | = N[∅] × N[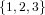 ] ∪ N[ ] ∪ N[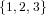 ] × N[∅] ] × N[∅] | |
|
| ∪ N[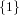 ] × N[ ] × N[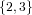 ] ∪ N[ ] ∪ N[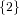 ] × N[ ] × N[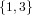 ] ∪ N[ ] ∪ N[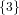 ] × N[ ] × N[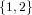 ] ] | |
|
| ∪ N[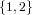 ] × N[ ] × N[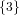 ] ∪ N[ ] ∪ N[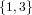 ] × N[ ] × N[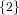 ] ∪ N[ ] ∪ N[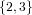 ] × N[ ] × N[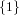 ] ] | |
|
| = 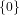 × ×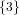 ∪ ∪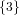 × ×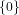 | |
|
| ∪ × × ∪ ∪ × × ∪ ∪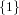 × ×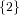 | |
|
| ∪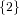 × ×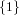 ∪ ∪ × × ∪ ∪ × × | |
|
| = 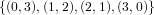 | | |
and thus card(N2[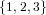 ]) = 4 instead of the expected 8.
]) = 4 instead of the expected 8.
This has some consequence for the representation of the product of species. We
must explicitly make the pairs disjoint by tagging them. According to (37) we tag
the parts by the pair (U1,U2) which is given through the Subset species.
174⟨representation: Times 174⟩≡ (175a)
Rep == Record(tag: Subset L, left: F L, right: G L);
Uses Subset 136.
The tag tells something about the split of the input set s of the function
structures.
ToDo ⊲ 26 ⊳ rhx ⊲ 17 ⊳ 19-Aug-2006: Do we need some functionality to access
the internal structure, i. e., should we be able to return a structure of type
F(
L) from
a given structure
Times(F, G)?
Type Constructor
Times
Description
Product of combinatorial species.
175a⟨dom: Times 175a⟩≡ (55)
Times(
F: SPECIES,
G: SPECIES
)(L: LabelType): CombinatorialSpecies(L) == add {
⟨representation: Times 174⟩
import from Rep;
⟨implementation: Times 175b⟩
}
Defines:
Times, used in chunks 442, 455, 640, 642–48, 650, 652, 655, 658, 719, 721, 723, and 732.
Uses CombinatorialSpecies 71, LabelType 62, and SPECIES 55.
175b⟨implementation: Times 175b⟩≡ (175a) 175c ⊳
(tw: TextWriter) << (x: %): TextWriter == {
import from String;
tw << "(" << rep(x).left << ", " << rep(x).right << ")";
}
Uses String 65.
175c⟨implementation: Times 175b⟩+
≡ (175a) ⊲175b 177 ⊳
(x: %) = (y: %): Boolean == {
macro {X == rep x; Y == rep y}
(X.tag = Y.tag) and (X.left = Y.left) and (X.right = Y.right);
}
ToDo ⊲ 27 ⊳ mrx ⊲ 3 ⊳ The following documentation chunk is duplicate, it is the
same as in the
Plus constructor. However, I’m not quite sure how to reference. Very
likely, we should introduce a sub-sub-section. This duplication really should go away.
We have to create the objects generatingSeries, isomorphismTypeGeneratingSeries
and expression first, before we start initialization. For example, the following
variant would lead to a runtime error when a species is defined recursively:
-
-
generatingSeries: ExponentialGeneratingSeries == new();
set!(generatingSeries $ %, generatingSeries$F(L) + generatingSeries$G(L));
isomorphismTypeGeneratingSeries: OrdinaryGeneratingSeries == new();
set!(isomorphismTypeGeneratingSeries $ %,
isomorphismTypeGeneratingSeries $ F(L) +
isomorphismTypeGeneratingSeries $ G(L));
The reason is that Aldor would—due to the first set! instruction in the second
line above—descend to the initialization of F(L) and G(L) before initializing
isomorphismTypeGeneratingSeries.
Thus, we need to call init after defining all recursively generated constants, but
before using them.
The same situation occurs in the Plus constructor.
177⟨implementation: Times 175b⟩+
≡ (175a) ⊲175c 178 ⊳
generatingSeries: ExponentialGeneratingSeries == new();
isomorphismTypeGeneratingSeries: OrdinaryGeneratingSeries == new();
cycleIndexSeries: CycleIndexSeries == new();
expression: SpeciesExpression == new();
local init(): () == {
set!(
generatingSeries $ %,
generatingSeries $ F(L) * generatingSeries $ G(L)
);
set!(
isomorphismTypeGeneratingSeries $ %,
isomorphismTypeGeneratingSeries $ F(L) *
isomorphismTypeGeneratingSeries $ G(L)
);
set!(
cycleIndexSeries $ %,
cycleIndexSeries $ F(L) * cycleIndexSeries $ G(L)
);
set!(expression$%, expression$F(L) + expression$G(L));
}
init();
Uses CycleIndexSeries 330, ExponentialGeneratingSeries 316,
OrdinaryGeneratingSeries 311, and SpeciesExpression 430.
For the product of species we need to generate all decompositions of a set U into
subsets U1 and U2 such that U1 ∪ U2 = U and U1 ∩ U2 = U. Thus we can simply
iterate over all structures of the species of subsets.
Exchanging F and G in the input of Times does, of course, not yields identical
structures, i. e.Times is not commutative.
In order to avoid infinite recursion for recursively defined structures, we first
check whether the coefficient of the generating series that corresponds to the input
list u or v is zero. If it is, there is no need to recurse any further, since no structures
must be generated. Note that it is not sufficient to test whether the coefficient of the
generating series corresponding to the input list s is zero: infinite recursion may
result, if, for example, the coefficient corresponding to v vanishes, but not the
coefficient corresponding to u.
The domain ExponentialGeneratingSeries is implemented in such a way that a
series knows approximately about its order, thus, accessing the coefficient of the
series, will not lead to infinite recursion though the species and the generating series
are defined by the same equations.
178⟨implementation: Times 175b⟩+
≡ (175a) ⊲177 179 ⊳
structures(s: SetSpecies L): Generator % == {
zero? coefficient(generatingSeries$%, #s) => generate {};
import from I, Q, ExponentialGeneratingSeries;
macro c(F,n) == coefficient(generatingSeries$F(L), n);
generate {
for t in structures(s)$Subset(L) repeat {
u: SetSpecies L := t :: SetSpecies(L);-- the subset
v: SetSpecies L := complement t; -- its complement
zero? c(F, #u) or zero? c(G, #v) => iterate;
for x in structures(u)$F(L) repeat {
for y in structures(v)$G(L) repeat {
yield per [t, x, y];
}
}
}
}
}
Uses ExponentialGeneratingSeries 316, Generator 617, I 47, Q 47, SetSpecies 117,
and Subset 136.
ToDo ⊲ 28 ⊳ rhx ⊲ 18 ⊳ 27-Sep-2006: It might be a bit more efficient to export
a second function
-
-
structures: (I, List L) -> Generator %
so that
#s would have to be computed only once and passed down the hierarchy.
The isomorphismTypes in the product species are generated in a manner very
similar to the generation of the structures. In fact, we simply replace structures
by isomorphismTypes for all occurrences.
ToDo ⊲ 29 ⊳ mrx ⊲ 4 ⊳ 25-Dec-2006: Brendan Mc Kay’s
nauty produces a
canonical labelling for graphs. Maybe we should look at this.
179⟨implementation: Times 175b⟩+
≡ (175a) ⊲178
isomorphismTypes(s: SetSpecies L): Generator % == {
import from I, Q, ExponentialGeneratingSeries;
zero? coefficient(generatingSeries$%, #s) => generate {};
macro c(F,n) == coefficient(generatingSeries$F(L), n);
generate {
for t in isomorphismTypes(s)$Subset(L) repeat {
u: SetSpecies L := t :: SetSpecies(L);-- the subset
v: SetSpecies L := complement t; -- its complement
zero? c(F, #u) or zero? c(G, #v) => iterate;
for x in isomorphismTypes(u)$F(L) repeat {
for y in isomorphismTypes(v)$G(L) repeat {
yield per [t, x, y];
}
}
}
}
}
Uses ExponentialGeneratingSeries 316, Generator 617, I 47, Q 47, SetSpecies 117,
and Subset 136.
![(F ⋅G )[U] = ∑ F[U ]× G [U ]
(U ,U ) 1 2
1 2](combinat103x.png)
 = (F[σ1](f),G[σ2](g))](combinat104x.png)
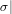 Ui is the restriction of σ on Ui, i = 1,2.
Ui is the restriction of σ on Ui, i = 1,2.
![N[U] = {cardU }](combinat106x.png)
 = n](combinat107x.png)
![νU : E [U ] → N [U], U ↦→ card U.](combinat108x.png)
) = νV(V) = cardV = n](combinat109x.png)
) = N [σ ](n) = n](combinat110x.png)
![μ : N[U] → E[U], cardU ↦→ U.
U](combinat111x.png)
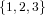 ]
]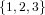 ]
] 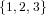 ]
] 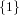 ]
] 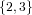 ]
] 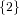 ]
] 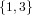 ]
] 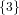 ]
] 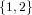 ]
]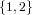 ]
] 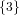 ]
] 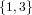 ]
] 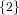 ]
] 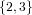 ]
] 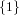 ]
]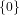
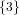
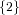
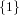
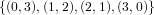
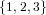 ]) = 4 instead of the expected 8.
]) = 4 instead of the expected 8.