[Home] [prev] [up] [next]     ((src/species.as))

8.5 Turn Some Existing Aldor Domains into Species

  8.5.1 The Set Species

8.5.1 The Set Species

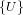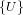Definition 8.5. [BLL98, p. 8] The species E of sets (french: ensemble) is defined by E[U] = {U } for any finite set U. For any bijection σ : U → V , E[σ] is given by mapping the only element U ∈ E[U] to the only element V ∈ E[V ].

Originally, we wanted to extend the existing Set constructor from the Aldor library. Unfortunately, Set does not guarantee that in

a: List L := [1,2,3];
s: Set  L := [l for l in a];
b: List L := [l for l in s];

a and b are identical.

From a mathematical point of view there is no problem at all. However, computationally, it might be desirable to be able to tell something about the order of the set elements, in order to go conveniently back and forth between Set and List. In fact, for SetSpecies we would like to be able to turn a list into a set in constant time, since in some cases we know that the list does not contain duplicate elements.

Since, we cannot access the internal data structure of Set, we cannot simply extend Set and thus must provide SetSpecies.

Since we currently do not need much of the functionality of Set and, in fact, SetSpecies should in many respects behave like the List data structure (not the combinatorial species), we provide only the functionality that is needed.

First of all, the following code should give a = b.

a: List L := [1,2,3];
s: SetSpecies L := set(a);
b: List L := s :: List(L);

Furthermore, for any F of type

(L: LabelType) -> CombinatorialSpecies L

and any s and t of type SetSpecies L with

(s :: List L) = (t :: List L)

we (want to) ensure that the lists [structures s] and [structures t] of type List F L are equal.

Such a deterministic behavior is vital for reliable ranking and unranking algorithms.

The argument against using List is that as combinatorial species List and SetSpecies are quite different. And, additionally, by using List we would lose the information that the list in question has no duplicate elements.

Note that SetSpecies and CombinatorialSpecies should be defined in the same file since they mutually depend on each other.

Type Constructor

SetSpecies

Usage

s: SetSpecies Integer := [3, 5, 2];
for x in structures(s) repeat stdout << x << newline;

Description

The Set constructor seen as a combinatorial species.

ToDo ⊲ 22 ⊳
rhx ⊲ 14 ⊳ 14-Oct-2006: SetSpecies needs more specification!!! In particular, a function

bracket: Tuple L -> %

as needed above is still not available and not even specified, but it should behave like:

bracket(t: Tuple L): % == {
  l: List L == [t];
  s: % := empty;
  while not empty? l repeat {
    s := union(first l, s);
    l := rest l;
  }
  per reverse! rep s;
}

For example, [1,3,5,2,5,1,3] gives the set [1,3,5,2], i. e., earlier elements survive.
117⟨dom: SetSpecies 117⟩≡   (55)
SetSpecies(L: LabelType): with {
        ⟨exports: SetSpecies 119⟩
} == List L add {
        Rep == List L;
        import from Rep;
        ⟨implementation: SetSpecies 122b⟩
}

Defines:
SetSpecies, used in chunks 78–80, 85–87, 91c, 92b, 100, 109–111, 124, 128, 131b, 132a, 139–42, 144c, 149, 157, 158, 163a, 169b, 170, 178, 179, 182a, 185, 186, 188, 189, 192, 455, 628, 632, 633b, 640, 644, 649, 650, 652, 654, 655, 657, 665, 707, 716, 719, 721, 723–25, and 727.

Uses LabelType 62.

Exports of SetSpecies

CombinatorialSpecies L;

empty?: % -> Boolean

#: % -> I

first: % -> L

first: (%, I) -> %

rest: % -> %

rest: (%, I) -> %

union: (L, %) -> %

empty: %

coerce: % -> List L

generator: % -> Generator L

cons: (L, %) -> % Adds a new element to the set.

set: List L -> % Turns a list into a set species.

119⟨exports: SetSpecies 119⟩≡   (117)  120 ⊳
CombinatorialSpecies L;

Uses CombinatorialSpecies 71.

Remember that # must not appear in the first column, otherwise it might be misinterpreted by the compiler as a system command.

120⟨exports: SetSpecies 119⟩+≡   (117)  ⊲119  121 ⊳
empty?: % -> Boolean;
 #: % -> I;
first: % -> L;
first: (%, I) -> %;
rest: % -> %;
rest: (%, I) -> %;
union: (L, %) -> %;
empty: %;
coerce: % -> List L;
generator: % -> Generator L;

Uses Generator 617 and I 47.

The following might lead to non-sets if applied to bad data.

Export of SetSpecies

cons: (L, %) -> %

Description

Adds a new element to the set.

The function inserts a new element in such a way that the new element will have index 1.

Remarks

The function does not check whether the element is already in the set and thus is potentially type-unsafe.

121⟨exports: SetSpecies 119⟩+≡   (117)  ⊲120  122a ⊳
cons: (L, %) -> %;

Export of SetSpecies

set: List L -> %

Description

Turns a list into a set species.

The function turns a list into a set without checking whether all elements in the list are different.

Remarks

The function does not check whether given list has pairwise different elements and thus is potentially type-unsafe.

122a⟨exports: SetSpecies 119⟩+≡   (117)  ⊲121
set: List L -> %;
122b⟨implementation: SetSpecies 122b⟩≡   (117)  122c ⊳
(x: %) = (y: %): Boolean == {
        import from I;
        #x ~= #y => false;
        for e in x repeat if not member?(e, rep y) then return false;
        true;
}

Uses I 47.
122c⟨implementation: SetSpecies 122b⟩+≡   (117)  ⊲122b  123a ⊳
first(x: %, n: I): % == per [e for e in rep x for i in 1..n];

Uses I 47.
123a⟨implementation: SetSpecies 122b⟩+≡   (117)  ⊲122c  123b ⊳
rest(x: %, n: I): % == if zero? n then x else rest(rest x, prev n);

Uses I 47.
123b⟨implementation: SetSpecies 122b⟩+≡   (117)  ⊲123a  123c ⊳
union(l: L, x: %): % == if member?(l, rep x) then x else cons(l, x);
123c⟨implementation: SetSpecies 122b⟩+≡   (117)  ⊲123b  123d ⊳
set(l: List L): % == {
#if Axiom
        --rhx: I didn’t want to create a new type ACSet just for this
        --rhx: one case.
#else
        assert(import from I, Set L; #l = #([e for e in l]$Set(L)));
#endif
        per l;
}

Uses I 47.
123d⟨implementation: SetSpecies 122b⟩+≡   (117)  ⊲123c  124a ⊳
coerce(x: %): List L == rep x;
124a⟨implementation: SetSpecies 122b⟩+≡   (117)  ⊲123d  124b ⊳
structures(s: SetSpecies L): Generator % == generate yield s;

Uses Generator 617 and SetSpecies 117.
124b⟨implementation: SetSpecies 122b⟩+≡   (117)  ⊲124a  124c ⊳
isomorphismTypes: SetSpecies L -> Generator % == structures;

Uses Generator 617 and SetSpecies 117.

The generating series is ex.

124c⟨implementation: SetSpecies 122b⟩+≡   (117)  ⊲124b  124d ⊳
generatingSeries: ExponentialGeneratingSeries == {
        import from Q, DataStream Z;
        (inv(fn) for fn in factorialStream) :: ExponentialGeneratingSeries;
}

Uses DataStream 386, ExponentialGeneratingSeries 316, Q 47, and Z 47.

And the isomorphism type generating series is 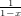1 1−-x.

124d⟨implementation: SetSpecies 122b⟩+≡   (117)  ⊲124c  125a ⊳
isomorphismTypeGeneratingSeries: OrdinaryGeneratingSeries == {
        (stream(1$Z)$DataStream(Z)) :: OrdinaryGeneratingSeries;
}

Uses DataStream 386, OrdinaryGeneratingSeries 311, and Z 47.

The cycle index series ZE of the species E of sets is given by

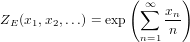( ) ∞∑ xn- ZE (x1,x2,...) = exp n n=1
(12)
For the workaround see ToDo 10.
125a⟨implementation: SetSpecies 122b⟩+≡   (117)  ⊲124d  125b ⊳
local cis(): CycleIndexSeries == BugWorkaround(
    CycleIndexSeries has with {exponentiate: % -> %}
){
        g: Generator P := generate {
                import from I, Z, Q, V, T, P;
                yield 0$P; -- constant term
                for n:I in 1.. repeat yield inv(n::Z) * (power(n::V, 1)::P);
        }
        import from DataStream P;
        exponentiate(g :: CycleIndexSeries);
}
cycleIndexSeries: CycleIndexSeries == cis();

Uses BugWorkaround 48, CycleIndexSeries 330, DataStream 386, Generator 617, I 47, Q 47, and Z 47.
125b⟨implementation: SetSpecies 122b⟩+≡   (117)  ⊲125a
import from String;
expression: SpeciesExpression == leaf("Set");

Uses SpeciesExpression 430 and String 65.

[Home] [prev] [up] [next]     ((src/species.as))