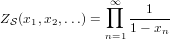8.4 Basic Species
8.4.1 The Empty Set Species
The species 1 (cf. [BLL98, p. 8]), characteristic of the empty set is defined by
![{
1[U] = {U }, if U = ∅,
∅, otherwise.](combinat36x.png) |
(3)
|
83⟨dom: EmptySetSpecies 83⟩≡ (55)
EmptySetSpecies(L: LabelType): CombinatorialSpecies L == {
CharacteristicSpecies(0$Integer)(L) add {
import from String;
expression: SpeciesExpression == leaf "EmptySetSpecies";
}
}
Defines:
EmptySetSpecies, used in chunks 194, 455, 458b, 629, 641–43, 645, and 647.
Uses CharacteristicSpecies 85, CombinatorialSpecies 71, Integer 66, LabelType 62,
SpeciesExpression 430, and String 65.
8.4.2 The Singleton Species
The species X (cf. [BLL98, p. 8]), characteristic of singletons is defined by
![{
{U} , if card U = 1,
X[U] = ∅, otherwise.](combinat37x.png) |
(4)
|
84⟨dom: SingletonSpecies 84⟩≡ (55)
SingletonSpecies(L: LabelType): CombinatorialSpecies L == {
CharacteristicSpecies(1$Integer)(L) add {
import from String;
expression: SpeciesExpression == leaf "SingletonSpecies";
}
}
Defines:
SingletonSpecies, used in chunks 88, 194, 455, 641–48, 650, 652, 658, 731, and 732.
Uses CharacteristicSpecies 85, CombinatorialSpecies 71, Integer 66, LabelType 62,
SpeciesExpression 430, and String 65.
8.4.3 The Characteristic Species
Type Constructor
CharacteristicSpecies
Usage
import from Integer;
EmptySetSpecies(L: LabelType): CombinatorialSpecies L == {
CharacteristicSpecies(0)(L) add;
}
SingletonSpecies(L: LabelType): CombinatorialSpecies L == {
CharacteristicSpecies(1)(L) add;
}
Description
The species that represents cardinality characteristics of sets.
According to [BLL98, p. 30], each species F gives rise canonically to an
enumerable family (Fn)n≥0 of species defined by setting for each n ∈ ℕ,
![{
F[U], if cardU = n,
Fn[U] = ∅, otherwise.](combinat38x.png) |
(5)
|
The species
Fn is said to be the species
F restricted to n.
If we denote by E the species of (finite) sets (given by the constructor SetSpecies)
then CharacteristicSpecies represents En. In other words, the domain
CharacteristicSpecies(L, n) can be thought of as the species SetSpecies(L)
restricted to n.
See also
EmptySetSpecies SingletonSpecies
86a⟨implementation: CharacteristicSpecies 86a⟩≡ (85) 86b ⊳
structures(s: SetSpecies L): Generator % == {
import from I;
generate if #s = nn then yield per s;
}
Uses Generator 617, I 47, and SetSpecies 117.
87c⟨implementation: CharacteristicSpecies 86a⟩+
≡ (85) ⊲87b 87d ⊳
(x: %) = (y: %): Boolean == rep x = rep y;
87d⟨implementation: CharacteristicSpecies 86a⟩+
≡ (85) ⊲87c 88 ⊳
(tw: TextWriter) << (x: %): TextWriter == {
import from L, String;
empty? rep x => tw << "nil";
empty? rest rep x => tw << first rep x;
tw << rep x;
}
Uses String 65.
8.4.4 The Species of Linear Orders
Definition 8.2. [BLL98, Chp. 1.1] The species L which fulfils the equation
L = 1 + X ⋅ L is called the species of linear orders. For any bijection σ :
U → V , with U = 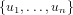 the bijection L[σ] : L[U] → L[V ] is given by
L[σ]([u1,…,ln]) = [σ(u1),…,σ(un)].
the bijection L[σ] : L[U] → L[V ] is given by
L[σ]([u1,…,ln]) = [σ(u1),…,σ(un)].
The species of linear order is also knows as the species of lists or the species of
sequences.
89⟨dom: LinearOrder 89⟩≡ (55)
LinearOrder(L: LabelType): with {
⟨exports: LinearOrder 90⟩
} == List L add {
Rep == List L;
import from Rep;
⟨implementation: LinearOrder 91b⟩
}
Defines:
LinearOrder, used in chunks 94, 100a, and 635.
Uses LabelType 62.
91a⟨exports: LinearOrder 90⟩+
≡ (89) ⊲90
coerce: % -> List L;
91b⟨implementation: LinearOrder 91b⟩≡ (89) 91c ⊳
coerce(x: %): List L == rep x;
91c⟨implementation: LinearOrder 91b⟩+
≡ (89) ⊲91b 92b ⊳
⟨generation of lists 92a⟩
structures(s: SetSpecies L): Generator % == generate {
for l in lists(s :: List L) repeat yield per l;
}
Uses Generator 617 and SetSpecies 117.
We generate all lists in a recursive fashion. We walk through the given list l and
then do the following for each element c of the list.
- Take out one element c from l.
- Generate all lists that do not contain c.
- For each of these generated lists, c is prepended as the first element and
the resulting list is yielded.
- Put c back to l in the same position as it was before.
92a⟨generation of lists 92a⟩≡ (91c)
local lists(l: List L): Generator List L == generate {
empty? l => yield l;
current := l;
c := first current;
for u in lists(rest l) repeat yield cons(c, u);
assert(not empty? current);
while not empty?(tmp := rest current) repeat {
c := first current;
setRest!(current, rest tmp); -- remove c from l
for u in lists l repeat yield cons(c, u);
setRest!(current, tmp); -- put c back into l
current := tmp;
}
}
Uses Generator 617.
The generating series is L(x) = 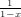 = 1 + x + x2 +
= 1 + x + x2 +  .
.
The isomorphism type generating series is also given by  (x) =
(x) = 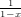 .
.
The cycle index series ZL of the species L of linear orders is given by
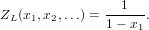 |
(6)
|
8.4.5 The Species of Cyclic Permutations
Let S[U] = 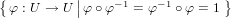 be the set of bijections on
U.
be the set of bijections on
U.
Definition 8.3. [BLL98, Chp. 1.1] The species C of cyclic permutations or oriented
cycles is defined by
![{ | }
C[U] = ϕ ∈ S[U]||∀u ∈ U : n = min(ϕk(u) = u)
| k>0](combinat46x.png) |
(7)
|
for any finite set
U with card(
U) =
n. In particular,
C[
∅] =
∅. For any bijection
σ :
U → V ,
C[
σ] is given by
C[
σ](
ϕ) =
σ ∘ ϕ ∘ σ−1.
The species of cyclic permutations is closely related to the species of linear orders
as can be seen by the generation of structures below.
ToDo ⊲ 20 ⊳ rhx ⊲ 12 ⊳
24-Mar-2007: Whenever the derivative of species is implemented then we should put
here the relation
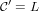 |
(8)
|
where
L is the
species of linear orders, see Example 1.4.7 in [BLL98].
96⟨dom: Cycle 96⟩≡ (55)
Cycle(L: LabelType): with {
⟨exports: Cycle 97⟩
} == List L add {
Rep == List L;
import from I, Rep;
⟨implementation: Cycle: auxiliary functions 103a⟩
⟨implementation: Cycle 98b⟩
}
Defines:
Cycle, used in chunks 104b, 109, 110b, 637, and 649.
Uses I 47 and LabelType 62.
Exports of Cycle
-
-
CombinatorialSpecies L;
-
-
coerce: % -> List L Coerce an oriented cycle to a list structure.
-
-
cycle: List L -> % Coerce a list structure into an oriented cycle.
Export of Cycle
coerce: % -> List L
Description
Coerce an oriented cycle to a list structure.
98a⟨exports: Cycle 97⟩+
≡ (96) ⊲97 99a ⊳
coerce: % -> List L;
98b⟨implementation: Cycle 98b⟩≡ (96) 99b ⊳
coerce(x: %): List L == rep x;
Export of Cycle
cycle: List L -> %
Description
Coerce a list structure into an oriented cycle.
ToDo ⊲ 21 ⊳ rhx ⊲ 13 ⊳ 23-Mar-2007: Maybe this is a dangerous function and
should be avoided. The question is, how canonical the representation is and how
complex this function should be. It currently is
O(1), but I am not sure that it is
usually doable in that time. This function is similar to
set. And we deliberately do
not call it
coerce.
99a⟨exports: Cycle 97⟩+
≡ (96) ⊲98a
cycle: List L -> %;
99b⟨implementation: Cycle 98b⟩+
≡ (96) ⊲98b 100a ⊳
cycle(l: List L): % == per l;
We can generate all cycles by taking away from s one element u, generate all
possible lists of the remaining elements and putting u as the first element of all these
generated lists.
100a⟨implementation: Cycle 98b⟩+
≡ (96) ⊲99b 100b ⊳
structures(s: SetSpecies L): Generator % == generate {
import from LinearOrder L;
if not empty? s then {
l: List L := s :: List L;
u := first l;
for t in structures(set rest l)$LinearOrder(L) repeat {
yield per cons(u, t :: List L);
}
}
}
Uses Generator 617, LinearOrder 89, and SetSpecies 117.
The isomorphism types of cyclic permutations are like those of LinearOrder or
SetSpecies, except that there is no structure on the empty set.
The generating series is
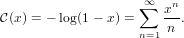 |
(9)
|
We know that the order of the series is 1 and therefore use the function new to
create the series and tell about the order.
The isomorphism type generating series is given by 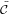 (x) =
(x) = 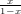 .
.
The cycle index series ZC of the species C of permutations is given by
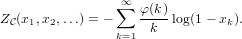 |
(10)
|
Since log(1 − x) = −∑
m=1∞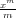 we can easily derive
we can easily derive
| ZC(x1,x2,…) | = ∑
k=1∞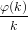 ∑
m=1∞ ∑
m=1∞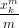 | |
|
| = ∑
n=1∞∑
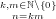 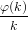 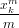 | |
|
| = ∑
n=1∞ ∑
k|nϕ(k)xkn∕k. ∑
k|nϕ(k)xkn∕k. | | |
We implement the last form of the sum, but we rather sum over all m = n∕k, because
in that way addition to p always adds bigger terms (in the term order on T)
later.
The following function generates all coefficients of the series. It starts with index
0.
Let us start with an auxiliary function for cisCoefficient which is the inverse of
factor, i. e., multiply converts a prime power product into the corresponding
integer.
103b⟨implementation: Cycle: cisCoefficient 103b⟩≡ (103a) 104a ⊳
local multiply(k: PrimePowerProduct): I == {
r: I := 1;
for ep in k repeat {(e, p) := ep; r := r * p^e}
r;
}
Uses I 47 and PrimePowerProduct 307.
For the workaround see ToDo 10.
104a⟨implementation: Cycle: cisCoefficient 103b⟩+
≡ (103a) ⊲103b
local cisCoefficient(n: I): P == BugWorkaround(
PrimePowerProduct has with {
divisors: % -> Generator %;
/: (%, %) -> %;
}
){
import from Z, V, SmallIntegerTools;
nn: PrimePowerProduct := factor n;
p: P := 0;
for m in divisors nn repeat {
k: PrimePowerProduct := nn/m;
q: Q := (eulerPhi(k) :: Z) / (n :: Z);
xk: V := multiply(k) :: V;
t: T := power(xk, multiply m);
p := [q, t]$P + p;
}
p;
}
Uses BugWorkaround 48, Generator 617, I 47, PrimePowerProduct 307, Q 47,
SmallIntegerTools 555, and Z 47.
8.4.6 The Species of Permutations
Definition 8.4. [BLL98, Chp. 1.1] The species S of permutations (bijective
endofunctions) is defined by S[U] = 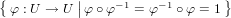 for
any finite set U. For any bijection σ : U → V , S[σ] is given by S[σ](ϕ) =
σ ∘ ϕ ∘ σ−1.
for
any finite set U. For any bijection σ : U → V , S[σ] is given by S[σ](ϕ) =
σ ∘ ϕ ∘ σ−1.
The species of permutations is closely related to the species of linear orders. However,
their isomorphism types are different and, therefore, we cannot use List as the
representation but rather have to use the following in accordance with the
representation of Partition. For the generation of isomorphism types we
can easily borrow from the code for Partition. In fact, each list in the
array presents a cycle in the cycle decomposition of a given permutation.
106⟨dom: Permutation 106⟩≡ (55)
Permutation(L: LabelType): with {
⟨exports: Permutation 107⟩
} == add {
⟨representation: Permutation 105⟩
import from Rep;
⟨implementation: Permutation: auxiliary functions 110b⟩
⟨implementation: Permutation 108b⟩
}
Defines:
Permutation, used in chunks 54, 114, 639, and 649.
Uses LabelType 62.
Exports of Permutation
-
-
CombinatorialSpecies L;
-
-
coerce: % -> Array List L Coerces internal representation to an array of lists.
-
-
coerce: % -> SetSpecies Cycle L Coerces internal representation to a set of
cycles.
Export of Permutation
coerce: % -> Array List L
Description
Coerces internal representation to an array of lists.
Export of Permutation
coerce: % -> SetSpecies Cycle L
Description
Coerces internal representation to a set of cycles.
Here we use the fact that S = E ∘C, where C is the species of cyclic permutations,
i. e., we simulate the generic generation of structures as it is done in Compose.
However, owing to the nature of the first and second argument of ∘ from above,
it is sufficient to produce an array and not a triple as in the generic case.
The following function is almost identical to the one given in the implementation
of Compose, except that in the return type we change from SetSpecies to Array.
And G is List (which represents Cycle) here.
110b⟨implementation: Permutation: auxiliary functions 110b⟩≡ (106)
local structures(
i: I,
pi: Array List L
): Generator Array List L == generate {
import from Cycle L;
i = #pi => yield new(i)$Array(List L);
s: SetSpecies L := set pi.i;
for g in structures(s)$Cycle(L) repeat {
for e in structures(next i, pi) repeat {
e.i := g :: List(L);
yield e;
}
}
}
Uses Array 599, Cycle 96, Generator 617, I 47, and SetSpecies 117.
The isomorphism types of the species of permutations are, in fact, integer
partitions, i. e., the same as isomorphism types of Partition.
The generating series is 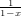 .
.
And the isomorphism type generating series is given by (192). The following code
uses the right hand side of this formual.
For the workaround see ToDo 10.
The cycle index series ZS of the species S of permutations is given by
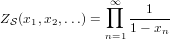 |
(11)
|
For the workaround see ToDo 10.
113b⟨implementation: Permutation 108b⟩+
≡ (106) ⊲113a 113c ⊳
(tw: TextWriter) << (x: %): TextWriter == tw << rep x;
113c⟨implementation: Permutation 108b⟩+
≡ (106) ⊲113b 114 ⊳
(x: %) = (y: %): Boolean == rep x = rep y;
![{
1[U] = {U }, if U = ∅,
∅, otherwise.](combinat36x.png)
![{
1[U] = {U }, if U = ∅,
∅, otherwise.](combinat36x.png)
![{
{U} , if card U = 1,
X[U] = ∅, otherwise.](combinat37x.png)
![{
F[U], if cardU = n,
Fn[U] = ∅, otherwise.](combinat38x.png)
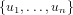 the bijection L[σ] : L[U] → L[V ] is given by
L[σ]([u1,…,ln]) = [σ(u1),…,σ(un)].
the bijection L[σ] : L[U] → L[V ] is given by
L[σ]([u1,…,ln]) = [σ(u1),…,σ(un)].
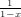 = 1 + x + x2 +
= 1 + x + x2 +  .
.  (x) =
(x) = 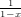 .
.
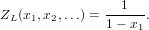
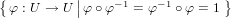 be the set of bijections on
U.
be the set of bijections on
U.
![{ | }
C[U] = ϕ ∈ S[U]||∀u ∈ U : n = min(ϕk(u) = u)
| k>0](combinat46x.png)
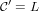
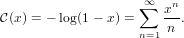
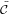 (x) =
(x) = 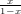 .
.
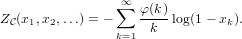
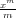 we can easily derive
we can easily derive
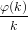 ∑
m=1∞
∑
m=1∞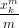
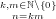
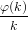
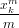
 ∑
k|nϕ(k)xkn∕k.
∑
k|nϕ(k)xkn∕k.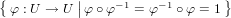 for
any finite set U. For any bijection σ : U → V , S[σ] is given by S[σ](ϕ) =
σ ∘ ϕ ∘ σ−1.
for
any finite set U. For any bijection σ : U → V , S[σ] is given by S[σ](ϕ) =
σ ∘ ϕ ∘ σ−1.
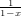 .
.