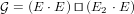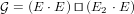24.13 Test Functorial Composition
Simple graphs can be described by as a functorial composite of subsets ℘ = E ⋅E
and subsets of 2-element sets ℘[2] = E2 ⋅ E,
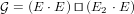 |
(188)
|
where E is the species of sets and E2 the species of 2-element sets, see [BLL98,
Chp. 2.2].
The values for the cycle indicator series are taken from [BLL98, Appendix 2,
Table 6].
655⟨test Functorial Compose 655⟩≡ (626)
testFunctorialCompose(): () == {
macro {
CS == CombinatorialSpecies;
E == SetSpecies;
E2 == RestrictedSpecies(E, 2);
WP == Subset;
P2 == Times(E2, E);
}
SimpleGraph(L: LabelType): CS L == FunctorialCompose(WP, P2)(L) add;
import from Integer, Array Integer;
check(
SimpleGraph,
[1, 1, 2, 8, 64, 1024, 32768, 2097152, 268435456, 68719476736],
[1,1,2,4,11,34,156, 1044, 12346, 274668],
[
1,
x(1,1),
x(1,2)+x(2,1),
(4/3)*x(1,3)+2/1*x(1,1)*x(2,1)+2/3*x(3,1),
(8/3)*x(1,4)+4/1*x(1,2)*x(2,1)+4/3*x(1,1)*x(3,1)
+2/1*x(2,2)+x(4,1),
128/15*x(1,5)+32/3*x(1,3)*x(2,1)+8/3*x(1,2)*x(3,1)
+2/1*x(1,1)*x(4,1)+8/1*x(1,1)*x(2,2)+4/3*x(2,1)*x(3,1)
+4/5*x(5,1),
2048/45*x(1,6)+128/3*x(1,4)*x(2,1)+64/9*x(1,3)*x(3,1)
+4/1*x(1,2)*x(4,1)+8/5*x(1,1)*x(5,1)+32/3*x(2,3)
+32/1*x(1,2)*x(2,2)+16/9*x(3,2)+16/3*x(1,1)*x(2,1)*x(3,1)
+4/1*x(2,1)*x(4,1)+4/3*x(6,1)
]
);
}
Uses Array 599, CombinatorialSpecies 71, FunctorialCompose 191a, Integer 66,
LabelType 62, RestrictedSpecies 127, SetSpecies 117, Subset 136, and Times 175a.
ToDo ⊲ 87 ⊳BUG! ⊲ 5 ⊳ rhx ⊲ 68 ⊳ 13-Feb-2007: CompilerBug. The
Aldor
compiler 1.0.2 does not produce a different (anonymous) function for each iteration.
657⟨test CompilerBug 657⟩≡ (626)
testCompilerBug(): () == {
setS: CycleIndexSeries := cycleIndexSeries $ SetSpecies(Integer);
set1s: DataStream P := stream generator(setS::DataStream(P));
set1s.0 := 0;
set1: CycleIndexSeries := set1s::CycleIndexSeries;
set2s: DataStream P := stretch(set1, 2)::DataStream(P);
set2s := map((p: P): P +-> inv(2)*p)(set2s);
set2: CycleIndexSeries := set2s::CycleIndexSeries;
assertEquals(Array P,
[0, x(1), inv(2)*x(1,2)+inv(2)*x(2),
inv(6)*x(1,3)+inv(2)*x(1)*x(2)+inv(3)*x(3)],
[coefficient(set1, n) for n: I in 0..3]);
assertEquals(Array P,
[0, 0, inv(2)*x(2),0, inv(4)*x(2,2)+inv(4)*x(4)],
[coefficient(set2, n) for n: I in 0..4]);
#if CompilerBug13Feb2007
g: Generator CycleIndexSeries := generate {
for k: I in 1..2 repeat {
d: DataStream P := stretch(set1, k)::DataStream(P);
s := map((p: P): P +-> inv(k::Z)*p)(d);
yield s::CycleIndexSeries;
}
}
#else
local div(k: I)(p: P): P == inv(k::Z)*p;
g: Generator CycleIndexSeries := generate {
for k: I in 1..2 repeat {
d: DataStream P := stretch(set1, k)::DataStream(P);
s := map(div k)(d);
yield s::CycleIndexSeries;
}
}
#endif
a: Array CycleIndexSeries := [g];
assertEquals(Array P,
[coefficient(set1, n) for n: I in 0..4],
[coefficient(a.0, n) for n: I in 0..4]);
assertEquals(Array P,
[coefficient(set2, n) for n: I in 0..4],
[coefficient(a.1, n) for n: I in 0..4]);
}
Uses Array 599, CycleIndexSeries 330, DataStream 386, Generator 617, I 47,
Integer 66, SetSpecies 117, and Z 47.
Unfortunately, the following code compiles in Aldor 1.0.2, but gives a
segmentation fault when run. Thus is not yet included.
658⟨NOTYET: test SpeciesCollection 658⟩≡
testSpeciesCollection(): () == {
macro {
X == SingletonSpecies;
+ == Plus;
* == Times;
}
import from Integer, Array Integer;
A(L: LabelType): CombinatorialSpecies L == (X + B*B*B)(L) add;
B(L: LabelType): CombinatorialSpecies L == (X + A*A)(L) add;
T(L: LabelType): CombinatorialSpecies L == (X + T*T)(L) add;
species: List SPECIES == [A, B, T, SingletonSpecies];
local cnt(S: SPECIES, n: MachineInteger): Integer == {
s: ExponentialGeneratingSeries := generatingSeries$S(Integer);
count(s, n);
}
import from Integer, MachineInteger;
s1: List Integer := [cnt(S, 1) for S in species];
s5: List Integer := [cnt(S, 5) for S in species];
assertEquals(List Integer, [1,1,1,1], s1);
assertEquals(List Integer, [360,720,1680,0], s5);
}
Uses Array 599, CombinatorialSpecies 71, ExponentialGeneratingSeries 316,
Integer 66, LabelType 62, MachineInteger 67, Plus 166a, SingletonSpecies 84,
SPECIES 55, and Times 175a.