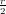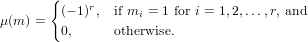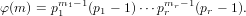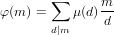21 Functions on 32-bit Integers
This file implements a number of functions on integers that fit into 32
bits.
In particular, it allows (non-probabilistic) primality testing, factorization of all
(32-bit) MachineInteger (−231 ≤ x < 231) by using trial division with the sequence
of 16-bit primes.
The functions are tested in test/sitools/sitools.as.nw.
554⟨* 13⟩+
≡ ⊲535 569a ⊳
-------------------------------------------------------------------
----
---- Combinat
---- Copyright (C) Ralf Hemmecke <ralf@hemmecke.de>
---- svn co svn://svn.risc.uni-linz.ac.at/hemmecke/combinat/
----
-------------------------------------------------------------------
#include "combinat"
⟨pkg: SmallIntegerTools 555⟩
Type Constructor
SmallIntegerTools
Description
Provides factorization of all positive integers smaller than 231.
Exports of SmallIntegerTools
-
-
nextPrime: MachineInteger -> MachineInteger Returns the closest prime bigger than the
given one.
-
-
previousPrime: MachineInteger -> MachineInteger Returns the closest prime smaller
than the given one.
-
-
prime?: MachineInteger -> Boolean Primality test.
-
-
sqrt: MachineInteger -> MachineInteger Integer root.
-
-
factor: MachineInteger -> SparseIndexedPowerProduct(I, I) Factors positive integer
smaller than 231.
-
-
moebiusMu: SparseIndexedPowerProduct(I, I) -> MachineInteger Compute the Möbius
μ function.
-
-
eulerPhi: SparseIndexedPowerProduct(I, I) -> MachineInteger Compute the Euler ϕ
function.
Export of SmallIntegerTools
nextPrime: MachineInteger -> MachineInteger
Description
Returns the closest prime bigger than the given one.
557b⟨implementation: SmallIntegerTools 557b⟩≡ (555) 558b ⊳
nextPrime(n: I): I == {
import from SmallIntegerPrimes, Array I;
n < maxPrime => {
(found?, i) := binarySearch(n, primes);
i < 0 => primes.0; -- first prime
assert(i < prev(#primes));
primes.(next i);
}
p: I := if even? n then n+1 else n+2;
while p <= max$I repeat {
prime?(p) $ % => return p;
p := p + 2;
}
return 0;
}
Uses Array 599, I 47, and SmallIntegerPrimes 536.
558b⟨implementation: SmallIntegerTools 557b⟩+
≡ (555) ⊲557b 559b ⊳
previousPrime(n: I): I == {
import from SmallIntegerPrimes, Array I;
n <= 2 => never;
n = 3 => 2;
p: I := if even? n then n-1 else n-2;
while n > maxPrime repeat {
prime?(p) $ % => return p;
p := p - 2;
}
(found?, i) := binarySearch(n, primes);
primes.i;
}
Uses Array 599, I 47, and SmallIntegerPrimes 536.
Export of SmallIntegerTools
prime?: MachineInteger -> Boolean
Usage
macro I == MachineInteger;
n: I := max;
assert(prime? n);
n: I := 2^30 + 3;
assert(prime? n);
Description
Primality test.
559b⟨implementation: SmallIntegerTools 557b⟩+
≡ (555) ⊲558b 561 ⊳
prime?(n: I): Boolean == {
import from SmallIntegerPrimes, Array I;
n < 2 => false;
(found?, i) := binarySearch(n, primes);
found? => true;
i < prev #primes => false;
k := sqrt n;
-- now we must use trial division for all primes up to k
for p in primes while p <= k repeat zero?(n rem p) => return false;
true;
}
Uses Array 599, I 47, and SmallIntegerPrimes 536.
Export of SmallIntegerTools
sqrt: MachineInteger -> MachineInteger
Usage
macro I == MachineInteger;
n: I := 2^30 + 3;
k: I := sqrt n;
assert(k = 2^15);
n := 2^30 - 35;
k := sqrt n;
assert(k = 2^15 -1);
Description
Integer root.
For an integer 0 ≤ n < 231 the function returns k = ⌊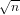 ⌋.
⌋.
The algorithm loops over the bits of the result starting with the biggest and
adjusts them. If n = ∑
i=0rni2i with ni ∈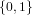 and nr = 1 then the highest bit in k
appears at position s = ⌊
and nr = 1 then the highest bit in k
appears at position s = ⌊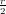 ⌋. We take 2s as as starting value and add more bits to the
result by checking whether the square of the result will become bigger than n.
⌋. We take 2s as as starting value and add more bits to the
result by checking whether the square of the result will become bigger than n.
561⟨implementation: SmallIntegerTools 557b⟩+
≡ (555) ⊲559b 562b ⊳
sqrt(n: I): I == {
n < 0 => -1;
zero? n or one? n => n;
s := shift(length(n) - 1, -1);
k: I := shift(1, s);
k*k = n => return k;
assert(k*k < n);
nextbit: I := shift(k, -1); -- k/2
while not zero? nextbit repeat {
k := k + nextbit; -- set bit
if k > 46340 then { -- avoid 32bit squaring overflow
k := k - nextbit; -- clear bit
} else {
k2 := k*k;
k2 = n => return k;
if k2 > n then k := k - nextbit; -- clear bit
}
nextbit := shift(nextbit, -1); -- nextbit/2
}
k;
}
Uses I 47.
Export of SmallIntegerTools
factor: MachineInteger -> SparseIndexedPowerProduct(I, I)
Description
Factors positive integer smaller than 231.
The following is basically an implementation of Algorithm A of Section 4.5.4 in
[Knu69], i. e., it uses trial division with a sequence of all 16-bit primes as division
candidates.
562b⟨implementation: SmallIntegerTools 557b⟩+
≡ (555) ⊲561 564b ⊳
factor(x: I): SparseIndexedPowerProduct(I, I) == {
t: SparseIndexedPowerProduct(I, I) := 1;
import from SmallIntegerPrimes, Array I;
default {y: I; r: I}
for p in primes repeat {
exponent := 0;
(y, r) := divide(x, p);
while zero? r repeat {
exponent := exponent + 1;
x := y;
(y, r) := divide(x, p);
}
if exponent > 0 then t := power(p, exponent) * t;
one? x => return t;
y <= p => return power(x, 1) * t; -- x is prime
}
never;
}
Uses Array 599, I 47, SmallIntegerPrimes 536, and SparseIndexedPowerProduct 506.
Export of SmallIntegerTools
moebiusMu: SparseIndexedPowerProduct(I, I) -> MachineInteger
Description
Compute the Möbius μ function.
The following function uses formula (4.57) of [GKP94]. If m = p1m1p2m2…prmr is
the factorization of m ∈ ℕ into distinct prime factors p1,…,pr then the Möbius
function is
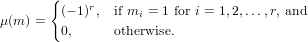 |
(182)
|
This includes in particular the case μ(1) = 1.
Export of SmallIntegerTools
eulerPhi: SparseIndexedPowerProduct(I, I) -> MachineInteger
Description
Compute the Euler ϕ function.
The Euler ϕ or totient function ϕ(m) encodes the number of divisors of m that are
relatively prime to m. See, for example, [GKP94, Chp. 4.9].
It is defined as ϕ(1) = 1 and ϕ(pk) = pk − pk−1 for any prime number p and any
integer k ≥ 1. Furthermore, ϕ is multiplicative, i. e., ϕ(m1m2) = ϕ(m1)ϕ(m2) if
gcd(m1,m2) = 1. If m = p1m1p2m2…prmr is the factorization of m ∈ ℕ into
distinct prime factors p1,…,pr then the Euler totient function is defined by
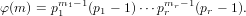 |
(183)
|
It is known that
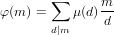 |
(184)
|
where
μ is the
Möbius function.
567⟨implementation: SmallIntegerTools 557b⟩+
≡ (555) ⊲564b
eulerPhi(t: SparseIndexedPowerProduct(I, I)): I == {
phi: I := 1;
for ep in t repeat {
(e, p) := ep;
phi := phi * p^(e-1) * (p-1)
}
phi;
}
Uses I 47 and SparseIndexedPowerProduct 506.
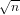 ⌋.
⌋.
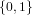 and
and