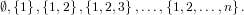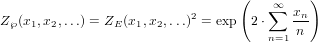8.8 The Species of Subsets
As given in [BLL98, Chp. 1.3], the species ℘ can be obtained by the
combinatorial equation
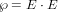 |
(16)
|
where E is the species of sets.
However, looking closer at the definition of multiplication F ⋅G of two species F
and G, (cf. (37)) one sees that subsets are needed. Thus we decided to implement the
species Subset as a basic species.
Type Constructor
Subset
Usage
s: SetSpecies Integer := set [1,2,3];
subsets: Subset Integer := structures(s);
for subset in subsets repeat stdout << subset << newline;
Description
The species of all subsets.
The structures of this species are all the subsets of the given set. Thus, its
isomorphism types are the non-negative numbers less than or equal to the size of the
input set.
We represent a subset as a set a (encoded by an array) together with a
characteristic vector indicating which elements a belong to the subset. Note that we
therefore depend on an—albeit arbitrary—ordering of the set.
ToDo ⊲ 23 ⊳ rhx ⊲
15 ⊳ 15-Mar-2007: The dependence on an order is a good argument to model
SetSpecies as we have it and additionally require that
LabelType is totally ordered.
Note, however, that such a total order on the label type
L is only a technical one and
should not be confused with the concept of
linear species as defined in [BLL98,
Chp. 5].
Let
-
-
r: Rep := ...
c: Integer := r.char;
a: Array L := r.set;
n := #a;
then r represents the subset that contains the element ai (i = 0,…,n) if the i-th bit in
the binary representation of c is set. The lowest bit has index 0. Note that we keep
the order of the elements from the input set.
If r = (c,a) with c = 11 = 8 + 2 + 1 = 010112, a = [1,2,3,4,5], and n = 5 then the
corresponding subset-complement pair is
![([2,4,5],[1,3]).](combinat69x.png) |
(17)
|
For the generation of structures in Times we need the subset as well as its
complement. So we provide two functions coerce and complement that return the
subset and its complement, respectively.
139b⟨implementation: Subset 139b⟩≡ (136) 140b ⊳
coerce(x: %): SetSpecies L == {
u: SetSpecies L := empty;
c: Z := rep(x).char;
a: Array L := rep(x).set;
d: PrimitiveArray L := data a;
i: I := #a;
while not zero? i repeat {
i := prev i;
if bit?(c, i) then u := cons(d.i, u);
}
u;
}
Uses Array 599, I 47, SetSpecies 117, and Z 47.
Export of Subset
complement: % -> SetSpecies L
Description
Returns the complement of the subset.
140b⟨implementation: Subset 139b⟩+
≡ (136) ⊲139b 141a ⊳
complement(x: %): SetSpecies L == {
u: SetSpecies L := empty;
c: Z := rep(x).char;
a: Array L := rep(x).set;
d: PrimitiveArray L := data a;
i: I := #a;
while not zero? i repeat {
i := prev i;
if not bit?(c, i) then u := cons(d.i, u);
}
u;
}
Uses Array 599, I 47, SetSpecies 117, and Z 47.
141a⟨implementation: Subset 139b⟩+
≡ (136) ⊲140b 142a ⊳
structures(s: SetSpecies L): Generator % == generate {
⟨n := #s; a: Array L := [u for u in s]; 141b⟩
for c: Z in 0 .. shift(1, n) - 1 repeat yield per [c, a];
}
Uses Generator 617, SetSpecies 117, and Z 47.
We do not provide a function bracket: Generator L -> % for Array in an
Axiom context, and the Aldor version builds an intermediate list. So we fill the
array directly.
141b⟨n:= #s; a: Array L := [u for u in s]; 141b⟩≡ (141a 142a)
n: I := #s;
a: Array L := new n;
for u in s for i: I in 0.. repeat a.i := u;
Uses Array 599 and I 47.
Canonical representatives of subsets of a set  are
are
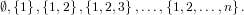 |
(18)
|
The above sequence corresponds to the numbers c = 2i − 1 for 0 ≤ i < n.
142a⟨implementation: Subset 139b⟩+
≡ (136) ⊲141a 142b ⊳
isomorphismTypes(s: SetSpecies L): Generator % == generate {
⟨n := #s; a: Array L := [u for u in s]; 141b⟩
c: Z := 0;
i: I := 0;
while i <= n repeat {
yield per [c, a];
c := shift(c, 1$I) + 1;
i := next i;
}
}
Uses Generator 617, I 47, SetSpecies 117, and Z 47.
The generating series is e2x.
The type generating series is e2x.
The cycle index series Z℘ of the species ℘ of subsets is given by 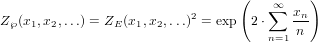 |
(19)
|
For the workaround see ToDo 10.
143b⟨implementation: Subset 139b⟩+
≡ (136) ⊲143a 144a ⊳
local cis(): CycleIndexSeries == BugWorkaround(
CycleIndexSeries has with {exponentiate: % -> %}
){
g: Generator P := generate {
import from I, Z, Q, V, T, P;
yield 0$P; -- constant term
for n:I in 1.. repeat yield [2/(n::Z) , power(n::V, 1)]$P;
}
import from DataStream P;
exponentiate(g :: CycleIndexSeries);
}
cycleIndexSeries: CycleIndexSeries == cis();
Uses BugWorkaround 48, CycleIndexSeries 330, DataStream 386, Generator 617, I 47,
Q 47, and Z 47.
144b⟨implementation: Subset 139b⟩+
≡ (136) ⊲144a 144c ⊳
(x: %) = (y: %): Boolean == {
(rep x).char = (rep y).char and
(rep x).set = (rep y).set;
}
![℘ [U ] = {S | S ⊆ U }
℘[U] = {S|S ⊆ U }](combinat67x.png)
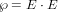
![([2,4,5],[1,3]).](combinat69x.png)
 are
are