11.2 Binomial Coefficients
Definition 11.1. Let n and k be integers and let k be non-negative. The
binomial coefficient 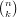 is defined by equation (160).
is defined by equation (160).
Note that equation (160) can also be used if n comes from an arbitrary ℚ-algebra.
Such a definition is not used in this file.
Export of MultinomialTools
binomial: (I, I) -> Integer
Usage
macro I == MachineInteger;
n: I := 22;
k: I := 7;
b: Integer := binomial(n, k);
Parameters
-
n: MachineInteger
-
A machine-size integer.
-
k: MachineInteger
-
A machine-size integer.
Description
Compute binomial coefficients.
For integers n and k the function binomial computes the binomial coefficient
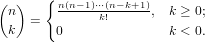 |
(160)
|
With this definition we follow [GKP94, pp. 154].
ToDo ⊲ 62 ⊳ mrx ⊲ 11 ⊳
04-Jan-2007: Why do you define the binomial coefficient only for machine size
integers?
Since binomial coefficients 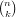 are often used while looping over the lower index k,
we remember the last computed coefficient and use it to compute
are often used while looping over the lower index k,
we remember the last computed coefficient and use it to compute 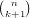 or
or
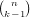 .
.
So we store (n,k,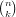 ) into the following record. This record is only used by the
function binomial directly. It is indirectly used by multinomial since it calls
binomial.
) into the following record. This record is only used by the
function binomial directly. It is indirectly used by multinomial since it calls
binomial.
Note, however, that the use of such a record currently forbids parallel execution,
since we have not implemented a sychronization of different processes accessing this
record.
370b⟨implementation: MultinomialTools 370a⟩+
≡ (367) ⊲370a 372 ⊳
binomial(n: I, k: I): Integer == {
default b: Integer; -- the return value
⟨binomial: special cases 371a⟩
⟨binomial: treat precomputed cases 374b⟩
free last; -- last computed binomial for n >= #halfPascalTriangle
if last.nn = n then {
⟨binomial: use last computed binomial 371b⟩
} else {
last.nn := n;
b := binomialUp(n, k, 0, 1); -- do the hard work
}
last.kk := k;
last.bb := b;
}
Uses I 47 and Integer 66.
The special cases do not need much explanation. The formula for negation of the
upper index can be found in [GKP94, p. 164].
371a⟨binomial: special cases 371a⟩≡ (370b)
k < 0 => 0;
zero? k => 1;
assert(k > 0);
n < 0 => {b := binomial(k - n - 1, k); even? k => b; -b}
n < k => 0;
assert(n > 0);
n < 2*k => binomial(n, n-k); -- symmetry
assert(n >= 2*k);
k = 1 => n :: Integer;
assert(k > 1);
Uses Integer 66.
371b⟨binomial: use last computed binomial 371b⟩≡ (370b)
lastk := last.kk;
if lastk = k then {
b := last.bb;
} else if lastk < k then {
b := binomialUp(n, k, lastk, last.bb);
} else {
b := binomialDown(n, k, lastk, last.bb);
}
Let us start with some a simple implementation of the binomial function. We are
going to improve it below and also precompute some values for a more efficient
version.
The function binomialUp builds on the fact that for i < n
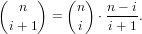 |
(161)
|
It assumes that b =  and computes
and computes 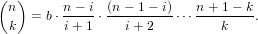 |
(162)
|
372⟨implementation: MultinomialTools 370a⟩+
≡ (367) ⊲370b 373 ⊳
binomialUp(n: I, k: I, i: I, b: Integer): Integer == {
assert(n > 0);
assert(k > 0);
assert(2*k <= n);
assert(i <= k);
assert(i >= 0);
while i < k repeat {
b := b * (n-i)::Z;
i := next i; -- i:=i+1
b := exquo(b, i :: Z);
}
b;
}
Uses exquo 365, I 47, Integer 66, and Z 47.
We can introduce a similar function which works downwards using a fact similar
to (161):
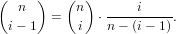 |
(163)
|
373⟨implementation: MultinomialTools 370a⟩+
≡ (367) ⊲372 380 ⊳
binomialDown(n: I, k: I, i: I, b: Integer): Integer == {
assert(n > 0);
assert(k > 0);
assert(2*k <= n);
assert(i >= k);
while k < i repeat {
b := b * i::Z;
i := prev i; -- i:=i-1
b := exquo(b, (n-i) :: Z);
}
b;
}
Uses exquo 365, I 47, Integer 66, and Z 47.
Up to n = 50 we store (half of) the Pascal triangle in an array of arrays.
[
[1], -- n=0
[1], -- n=1
[1, 2], -- n=2
[1, 3], -- n=3
[1, 4, 6], -- n=4
[1, 5, 10], -- n=5
[1, 6, 15, 20], -- n=6
...
]
|
The array for the constant halfPascalTriangle has been computed by the short
Maple program.
374a⟨Maple program to generate the table for the variable binom 374a⟩≡
line := proc(n) [seq(binomial(n, k), k=0..iquo(n,2))] end;
[seq(line(n), n=0..50)];
The values in the following array are such that halfPascalTriangle.n.k gives
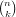 if 0 ≤ n ≤ 50, 0 ≤ k ≤
if 0 ≤ n ≤ 50, 0 ≤ k ≤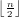 .
.
374b⟨binomial: treat precomputed cases 374b⟩≡ (370b)
free halfPascalTriangle;
import from PrimitiveArray Integer;
n < #halfPascalTriangle => halfPascalTriangle.n.k;
Uses Integer 66.
375⟨implementation: MultinomialTools: precomputed binomial coefficients 375⟩≡ (367)
import from PrimitiveArray Integer;
local halfPascalTriangle: Array PrimitiveArray Integer == [
[1],
[1],
[1, 2],
[1, 3],
[1, 4, 6],
[1, 5, 10],
[1, 6, 15, 20],
[1, 7, 21, 35],
[1, 8, 28, 56, 70],
[1, 9, 36, 84, 126],
[1, 10, 45, 120, 210, 252],
[1, 11, 55, 165, 330, 462],
[1, 12, 66, 220, 495, 792, 924],
[1, 13, 78, 286, 715, 1287, 1716],
[1, 14, 91, 364, 1001, 2002, 3003, 3432],
[1, 15, 105, 455, 1365, 3003, 5005, 6435],
[1, 16, 120, 560, 1820, 4368, 8008, 11440, 12870],
[1, 17, 136, 680, 2380, 6188, 12376, 19448, 24310],
[1, 18, 153, 816, 3060, 8568, 18564, 31824, 43758, 48620],
[1, 19, 171, 969, 3876, 11628, 27132, 50388, 75582, 92378],
[1, 20, 190, 1140, 4845, 15504, 38760, 77520, 125970, 167960,
184756],
[1, 21, 210, 1330, 5985, 20349, 54264, 116280, 203490, 293930,
352716],
[1, 22, 231, 1540, 7315, 26334, 74613, 170544, 319770, 497420,
646646, 705432],
[1, 23, 253, 1771, 8855, 33649, 100947, 245157, 490314, 817190,
1144066, 1352078],
[1, 24, 276, 2024, 10626, 42504, 134596, 346104, 735471, 1307504,
1961256, 2496144, 2704156],
[1, 25, 300, 2300, 12650, 53130, 177100, 480700, 1081575, 2042975,
3268760, 4457400, 5200300],
[1, 26, 325, 2600, 14950, 65780, 230230, 657800, 1562275, 3124550,
5311735, 7726160, 9657700, 10400600],
[1, 27, 351, 2925, 17550, 80730, 296010, 888030, 2220075, 4686825,
8436285, 13037895, 17383860, 20058300],
[1, 28, 378, 3276, 20475, 98280, 376740, 1184040, 3108105,
6906900, 13123110, 21474180, 30421755, 37442160, 40116600],
[1, 29, 406, 3654, 23751, 118755, 475020, 1560780, 4292145,
10015005, 20030010, 34597290, 51895935, 67863915, 77558760],
[1, 30, 435, 4060, 27405, 142506, 593775, 2035800, 5852925,
14307150, 30045015, 54627300, 86493225, 119759850, 145422675,
155117520],
[1, 31, 465, 4495, 31465, 169911, 736281, 2629575, 7888725,
20160075, 44352165, 84672315, 141120525, 206253075, 265182525,
300540195],
[1, 32, 496, 4960, 35960, 201376, 906192, 3365856, 10518300,
28048800, 64512240, 129024480, 225792840, 347373600,
471435600, 565722720, 601080390],
[1, 33, 528, 5456, 40920, 237336, 1107568, 4272048, 13884156,
38567100, 92561040, 193536720, 354817320, 573166440,
818809200, 1037158320, 1166803110],
[1, 34, 561, 5984, 46376, 278256, 1344904, 5379616, 18156204,
52451256, 131128140, 286097760, 548354040, 927983760,
1391975640, 1855967520, 2203961430, 2333606220],
[1, 35, 595, 6545, 52360, 324632, 1623160, 6724520, 23535820,
70607460, 183579396, 417225900, 834451800, 1476337800,
2319959400, 3247943160, 4059928950, 4537567650],
[1, 36, 630, 7140, 58905, 376992, 1947792, 8347680, 30260340,
94143280, 254186856, 600805296, 1251677700, 2310789600,
3796297200, 5567902560, 7307872110, 8597496600, 9075135300],
[1, 37, 666, 7770, 66045, 435897, 2324784, 10295472, 38608020,
124403620, 348330136, 854992152, 1852482996, 3562467300,
6107086800, 9364199760, 12875774670, 15905368710,
17672631900],
[1, 38, 703, 8436, 73815, 501942, 2760681, 12620256, 48903492,
163011640, 472733756, 1203322288, 2707475148, 5414950296,
9669554100, 15471286560, 22239974430, 28781143380,
33578000610, 35345263800],
[1, 39, 741, 9139, 82251, 575757, 3262623, 15380937, 61523748,
211915132, 635745396, 1676056044, 3910797436, 8122425444,
15084504396, 25140840660, 37711260990, 51021117810,
62359143990, 68923264410],
[1, 40, 780, 9880, 91390, 658008, 3838380, 18643560, 76904685,
273438880, 847660528, 2311801440, 5586853480, 12033222880,
23206929840, 40225345056, 62852101650, 88732378800,
113380261800, 131282408400, 137846528820],
[1, 41, 820, 10660, 101270, 749398, 4496388, 22481940, 95548245,
350343565, 1121099408, 3159461968, 7898654920, 17620076360,
35240152720, 63432274896, 103077446706, 151584480450,
202112640600, 244662670200, 269128937220],
[1, 42, 861, 11480, 111930, 850668, 5245786, 26978328, 118030185,
445891810, 1471442973, 4280561376, 11058116888, 25518731280,
52860229080, 98672427616, 166509721602, 254661927156,
353697121050, 446775310800, 513791607420, 538257874440],
[1, 43, 903, 12341, 123410, 962598, 6096454, 32224114, 145008513,
563921995, 1917334783, 5752004349, 15338678264, 36576848168,
78378960360, 151532656696, 265182149218, 421171648758,
608359048206, 800472431850, 960566918220, 1052049481860],
[1, 44, 946, 13244, 135751, 1086008, 7059052, 38320568, 177232627,
708930508, 2481256778, 7669339132, 21090682613, 51915526432,
114955808528, 229911617056, 416714805914, 686353797976,
1029530696964, 1408831480056, 1761039350070, 2012616400080,
2104098963720],
[1, 45, 990, 14190, 148995, 1221759, 8145060, 45379620, 215553195,
886163135, 3190187286, 10150595910, 28760021745, 73006209045,
166871334960, 344867425584, 646626422970, 1103068603890,
1715884494940, 2438362177020, 3169870830126, 3773655750150,
4116715363800],
[1, 46, 1035, 15180, 163185, 1370754, 9366819, 53524680,
260932815, 1101716330, 4076350421, 13340783196, 38910617655,
101766230790, 239877544005, 511738760544, 991493848554,
1749695026860, 2818953098830, 4154246671960, 5608233007146,
6943526580276, 7890371113950, 8233430727600],
[1, 47, 1081, 16215, 178365, 1533939, 10737573, 62891499,
314457495, 1362649145, 5178066751, 17417133617, 52251400851,
140676848445, 341643774795, 751616304549, 1503232609098,
2741188875414, 4568648125690, 6973199770790, 9762479679106,
12551759587422, 14833897694226, 16123801841550],
[1, 48, 1128, 17296, 194580, 1712304, 12271512, 73629072,
377348994, 1677106640, 6540715896, 22595200368, 69668534468,
192928249296, 482320623240, 1093260079344, 2254848913647,
4244421484512, 7309837001104, 11541847896480, 16735679449896,
22314239266528, 27385657281648, 30957699535776,
32247603683100],
[1, 49, 1176, 18424, 211876, 1906884, 13983816, 85900584,
450978066, 2054455634, 8217822536, 29135916264, 92263734836,
262596783764, 675248872536, 1575580702584, 3348108992991,
6499270398159, 11554258485616, 18851684897584, 28277527346376,
39049918716424, 49699896548176, 58343356817424,
63205303218876],
[1, 50, 1225, 19600, 230300, 2118760, 15890700, 99884400,
536878650, 2505433700, 10272278170, 37353738800, 121399651100,
354860518600, 937845656300, 2250829575120, 4923689695575,
9847379391150, 18053528883775, 30405943383200, 47129212243960,
67327446062800, 88749815264600, 108043253365600,
121548660036300, 126410606437752]
];
Uses Array 599 and Integer 66.
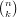 is defined by equation (160).
is defined by equation (160).
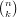 is defined by equation (160).
is defined by equation (160).
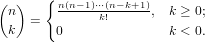
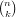 are often used while looping over the lower index k,
we remember the last computed coefficient and use it to compute
are often used while looping over the lower index k,
we remember the last computed coefficient and use it to compute 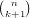 or
or
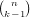 .
.
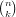 ) into the following record. This record is only used by the
function binomial directly. It is indirectly used by multinomial since it calls
binomial.
) into the following record. This record is only used by the
function binomial directly. It is indirectly used by multinomial since it calls
binomial.
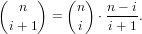
 and computes
and computes 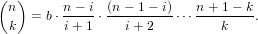
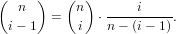
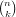 if 0 ≤ n ≤ 50, 0 ≤ k ≤
if 0 ≤ n ≤ 50, 0 ≤ k ≤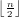 .
.