Definition 11.2. Let k1,…,kr be non-negative integers and n = ∑
i=1rki. The
multinomial coefficient 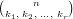 is defined by equation 164. It is undefined
for n
is defined by equation 164. It is undefined
for n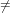 ∑
i=1rki.
∑
i=1rki.
Definition 11.2. Let k1,…,kr be non-negative integers and n = ∑
i=1rki. The
multinomial coefficient 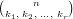 is defined by equation 164. It is undefined
for n
is defined by equation 164. It is undefined
for n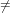 ∑
i=1rki.
∑
i=1rki.
Export of MultinomialTools
multinomial: List MachineInteger -> Integer
Usage
k: List I := [k1, ..., kr];
b: Integer := multinomial k;
Parameters
For each i the parameter ki is a (machine-size) integer.
Description
Compute multinomial coefficient.
For non-negative integers k1,…,kr the function multinomial computes the multinomial coefficient
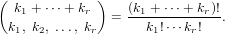 | (164) |
Remarks
We explicitly define multinomial([]) as 1.
Export of MultinomialTools
multinomial: (I, List I) -> Integer
Usage
macro I == MachineInteger;
k: List I := [k1, ..., kr];
n: I := 0;
for i in k repeat n := n + i;
b := multinomial(n, k);
Parameters
This must be ∑ i=1rki.
For each i the parameter ki is a non-negative integer.
Description
Compute multinomial coefficient.
For non-negative integers k1,…,kr with r > 0 the function multinomial computes the multinomial coefficient
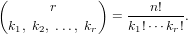 | (165) |
Remarks
Note that the output of the function is undefined for n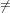 ∑
i=1rki. It is also
undefined, if the input list is empty.
∑
i=1rki. It is also
undefined, if the input list is empty.
Our implementation uses the following connection to binomial coefficients:
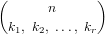 | = 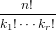 | (166) |
= 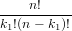 ⋅ ⋅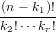 | (167) | |
= 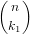 ⋅ ⋅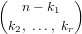 | (168) |