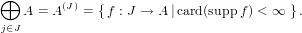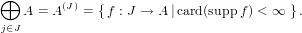SparseAdditiveArray

The domain IndexedFreeAdditiveCombinationType basically is an implementation of a polynomial domain that lacks multiplication. In fact, we can consider the type A as being an additive semigroup which is not necessarily commutative.

Type Constructor

SparseAdditiveArray

Description

Additive monoid of functions with finite support.

The domain constructor implements

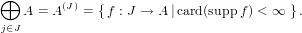⊕ A = A (J) = { f : J → A|card(supp f) < ∞ }.
j∈J

(177)

Parameters

A:: An additive monoid.
J:: A totally ordered index set.

489⟨dom: SparseAdditiveArray 489⟩≡   (462)
SparseAdditiveArray(
    A: with {
            zero?: % -> Boolean;
            +: (%, %) -> %;
    },
    J: TotallyOrderedType
): IndexedFreeAdditiveCombinationType(A, J) == add {
        macro Pair == Cross(A, J);
        Rep == List Pair;
        import from Pair, Rep;
        ⟨implementation: SparseAdditiveArray: auxiliary 491a⟩
        ⟨implementation: SparseAdditiveArray 490a⟩
}

Defines:
SparseAdditiveArray, used in chunks 501, 506, 733, 736a, 739, and 740.

Uses IndexedFreeAdditiveCombinationType 465 and TotallyOrderedType 571.

490c⟨implementation: SparseAdditiveArray 490a⟩+≡   (489)  ⊲490b  490d ⊳
bracket(a: A, j: J): % == {
        zero? a => 0;
        aj: Cross(A, J) := (a, j);
        per [aj];
}

490d⟨implementation: SparseAdditiveArray 490a⟩+≡   (489)  ⊲490c  491b ⊳
(x: %) + (y: %): % == {
        import from A, J, I;
        zero? x => y;
        zero? y => x;
        (xa, xj) := xm := leadingMonomial x;
        (ya, yj) := ym := leadingMonomial y;
        c := compare(xj, yj);
        c > 0 => TOPADD(xm, reductum x + y);
        c < 0 => TOPADD(ym, x + reductum y);
        a: A := xa + ya;
        z: % := reductum x + reductum y;
        if not zero? a then z := topAdd(a, xj, z);
        z;
}

Uses I 47.

The auxiliary function is a way to add a monomial when it is already known that j is bigger than any index in x.

491a⟨implementation: SparseAdditiveArray: auxiliary 491a⟩≡   (489)
macro TOPADD(m, x) == per cons(m, rep x);
local topAdd(a: A, j: J, x: %): % == {
        import from I;
        assert(zero? x or j > maxSupport x);
        assert(not zero? a);
        aj: Cross(A, J) := (a, j);
        TOPADD(aj, x);
}

Uses I 47.

491b⟨implementation: SparseAdditiveArray 490a⟩+≡   (489)  ⊲490d  491c ⊳
leadingMonomial(x: %): Cross(A, J) == {
        assert(not zero? x);
        first rep x;
}

491c⟨implementation: SparseAdditiveArray 490a⟩+≡   (489)  ⊲491b  491d ⊳
reductum(x: %): % == {
        assert(not zero? x);
        per rest rep x;
}

491d⟨implementation: SparseAdditiveArray 490a⟩+≡ (489) ⊲491c 492a ⊳
generator(x: %): Generator Cross(A, J) == generator rep x;

Uses Generator 617.

492a⟨implementation: SparseAdditiveArray 490a⟩+≡ (489) ⊲491d 492b ⊳
#(x: %): MachineInteger == # rep x;

Uses MachineInteger 67.

492b⟨implementation: SparseAdditiveArray 490a⟩+≡ (489) ⊲492a 492c ⊳
map(f: A -> A)(x: %): % == {
per [((a,j):=m; mm:=(f(a),j)) for m in x];
}

492c⟨implementation: SparseAdditiveArray 490a⟩+≡ (489) ⊲492b 492d ⊳
map(f: Cross(A,J) -> Cross(A,J))(x: %): % == per map(f) rep x;

492d⟨implementation: SparseAdditiveArray 490a⟩+≡ (489) ⊲492c
if A has with {-: (%, %) -> %; -: % -> %} then {
⟨implementation: SparseAdditiveArray: minus 493⟩
}

493⟨implementation: SparseAdditiveArray: minus 493⟩≡   (492d)
(x: %) - (y: %): % == {
        import from A, J, I;
        zero? x => -y;
        zero? y => x;
        (xa, xj) := xm := leadingMonomial x;
        (ya, yj) := ym := leadingMonomial y;
        c := compare(xj, yj);
        c > 0 => TOPADD(xm, reductum x - y);
        c < 0 => {ym := (-ya, yj); TOPADD(ym, x - reductum y);}
        a: A := xa - ya;
        z: % := reductum x - reductum y;
        if not zero? a then z := topAdd(a, xj, z);
        z;
}

Uses I 47.

17.2 SparseAdditiveArray