17.1 IndexedFreeAdditiveCombinationType
ToDo ⊲ 76 ⊳ rhx ⊲ 56 ⊳ 10-Jan-2007: This should be close to
IndexedFreeLinearCombinationType of the
Algebra library, but we do not
require a multiplication
and thus do not use
Linear in the name.
Type Constructor
IndexedFreeAdditiveCombinationType
Usage
macro A == Integer; -- coefficient type
macro J == MachineInteger; -- index type
SparseOrderedAdditiveArray(A, J): with {
IndexedFreeAdditiveCombinationType(A, J);
TotallyOrderedType;
} == add { ... }
Description
A category of weak polynomials.
Informally a domain that realizes IndexedFreeAdditiveCombinationType can be
seen as a polynomial domain A[J] that lacks multiplication and implements
subtraction only if A does.
The type IndexedFreeAdditiveCombinationType is the type of structures whose
elements are finite products of elements from A. It can be see as the monoid
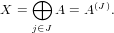 |
(173)
|
The semigroup structure of A lifts to X (see +). Also subtraction is lifted if it exists
in A.
Parameters
-
A:
-
An additive monoid that allows a zero test.
-
J:
-
An ordered (finite or infinite) index set.
Remarks
We do not require AbelianMonoid as the type of A since we do not necessarily
assume that the addition is commutative and since we want to be as minimal as
possible.
465⟨cat: IndexedFreeAdditiveCombinationType 465⟩≡ (462)
define IndexedFreeAdditiveCombinationType(
A: with {
zero?: % -> Boolean;
+: (%, %) -> %;
},
J: TotallyOrderedType
): Category == with {
⟨exports: IndexedFreeAdditiveCombinationType 468⟩
default {
⟨defaults: IndexedFreeAdditiveCombinationType 473b⟩
}
}
Defines:
IndexedFreeAdditiveCombinationType, used in chunks 489 and 496.
Uses TotallyOrderedType 571.
Exports of IndexedFreeAdditiveCombinationType
-
-
0: % Zero element.
-
-
zero?: % -> Boolean Zero test.
-
-
bracket: (A, J) -> % Construction of a monomial element.
-
-
+: (%, %) -> % Lifted addition.
-
-
leadingMonomial: % -> Cross(A, J) Returns the monomial with biggest index.
-
-
leadingCoefficient: % -> A Returns the coefficient of the monomial with biggest index.
-
-
reductum: % -> % Removes the monomial with biggest index.
-
-
maxSupport: % -> J Returns the biggest index of the support of the element.
-
-
generator: % -> Generator Cross(A, J) Generates coefficient-index pairs starting with
the biggest index.
-
-
#: % -> MachineInteger Returns the number of elements in the support.
-
-
map: (A -> A) -> % -> % Applies a function to all coefficients.
-
-
map: (Cross(A,J) -> Cross(A,J)) -> % -> % Applies a function to all monomials.
-
-
if A has with {-: (%, %) -> %; -: % -> %} then {
-
-
-: (%, %) -> % Lifted subtration.
-
-
-: % -> % Lifted negation.
-
-
}
-
-
if A has with {0: %} then {
-
-
apply: (%, J) -> A Returns the coefficient corresponding to the given index.
-
-
}
-
-
if A has PrimitiveType then PrimitiveType;
-
-
if A has TotallyOrderedType then TotallyOrderedType;
-
-
if A has OutputType and J has OutputType then OutputType;
468⟨exports: IndexedFreeAdditiveCombinationType 468⟩≡ (465) 469 ⊳
0: %;
469⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲468 470 ⊳
zero?: % -> Boolean;
470⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲469 471 ⊳
bracket: (A, J) -> %;
Export of IndexedFreeAdditiveCombinationType
+: (%, %) -> %
Description
Lifted addition.
The monoid structure of A lifts to X = A(J). Let a1 : J → A and a2 : J → A with
supp(a1) = I1 and supp(a2) = I2. Then a = a1 + a2 is defined as the function
a : J → A with
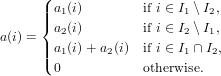 |
(175)
|
471⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲470 472 ⊳
+: (%, %) -> %;
Export of IndexedFreeAdditiveCombinationType
leadingMonomial: % -> Cross(A, J)
Description
Returns the monomial with biggest index.
Since each element f has finite support S, the function returns the pair (f(j),j) such
that j = maxS where the maximum is taken with respect to the given compare
function of the given index set J.
Remarks
The result of leadingMonomial(0) is undefined and may result in a runtime
exception.
472⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲471 473a ⊳
leadingMonomial: % -> Cross(A, J);
Export of IndexedFreeAdditiveCombinationType
leadingCoefficient: % -> A
Description
Returns the coefficient of the monomial with biggest index.
Since each element f has finite support S, the function returns f(j) for j = maxS
where the maximum is taken with respect to the given compare function of the given
index set J.
Remarks
The result of leadingCoefficient(0) is undefined and may result in a runtime
exception.
473a⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲472 474 ⊳
leadingCoefficient: % -> A;
473b⟨defaults: IndexedFreeAdditiveCombinationType 473b⟩≡ (465) 475b ⊳
leadingCoefficient(x: %): A == {
assert(not zero? x);
(a, j) := leadingMonomial x;
a;
}
Export of IndexedFreeAdditiveCombinationType
reductum: % -> %
Description
Removes the monomial with biggest index.
Since each element f has finite support S, the function returns the element g with
supp(g) = S ∖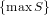 and f(j) = g(j) on the common support of f and
g.
and f(j) = g(j) on the common support of f and
g.
The maximum is taken with respect to the given compare function of the given index
set J.
Remarks
The result of reductum(0) is undefined and may result in a runtime exception.
474⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲473a 475a ⊳
reductum: % -> %;
Export of IndexedFreeAdditiveCombinationType
maxSupport: % -> J
Description
Returns the biggest index of the support of the element.
Since each element f has finite support S, the function returns j = maxS where the
maximum is taken with respect to the given compare function of the given index set
J.
Remarks
The result of maxSupport(0) is undefined and may result in a runtime
exception.
475a⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲474 476 ⊳
maxSupport: % -> J;
475b⟨defaults: IndexedFreeAdditiveCombinationType 473b⟩+
≡ (465) ⊲473b 479c ⊳
maxSupport(x: %): J == {
assert(not zero? x);
(a, j) := leadingMonomial x;
j;
}
478⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲477 479a ⊳
map: (A -> A) -> % -> %;
Export of IndexedFreeAdditiveCombinationType
map: (Cross(A,J) -> Cross(A,J)) -> % -> %
Description
Applies a function to all monomials.
Remarks
This function assumes that the given function that is applied to coefficient and
index does not destroy the order, i. e., we assume that in map(f,x) the function
f : A × J → A × J is monotone in its second argurment; if (a1′,j1′) = f(a1,j1)
and (a2′,j2′) = f(a2,j2) and j1 < j2 then j1′ < j2′.
479a⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲478 479b ⊳
map: (Cross(A,J) -> Cross(A,J)) -> % -> %;
Some functionality can only be implemented (and we do it as category defaults) if
the coefficient domain A provides enought functionality.
479b⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲479a 481c ⊳
if A has with {-: (%, %) -> %; -: % -> %} then {
⟨exports: IndexedFreeAdditiveCombinationType: minus 480a⟩
}
479c⟨defaults: IndexedFreeAdditiveCombinationType 473b⟩+
≡ (465) ⊲475b 481d ⊳
if A has with {-: (%, %) -> %; -: % -> %} then {
⟨defaults: IndexedFreeAdditiveCombinationType: minus 480b⟩
}
Export of IndexedFreeAdditiveCombinationType
-: (%, %) -> %
Description
Lifted subtration.
The monoid structure of A lifts to X = A(J). Let a1 : J → A and a2 : J → A with
supp(a1) = I1 and supp(a2) = I2. Then a = a1 − a2 is defined as the function
a : J → A with
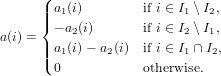 |
(176)
|
480a⟨exports: IndexedFreeAdditiveCombinationType: minus 480a⟩≡ (479b) 481a ⊳
-: (%, %) -> %;
480b⟨defaults: IndexedFreeAdditiveCombinationType: minus 480b⟩≡ (479c) 481b ⊳
(x: %) - (y: %): % == x + (-y);
481a⟨exports: IndexedFreeAdditiveCombinationType: minus 480a⟩+
≡ (479b) ⊲480a
-: % -> %;
481b⟨defaults: IndexedFreeAdditiveCombinationType: minus 480b⟩+
≡ (479c) ⊲480b
-(x: %): % == map(-$A)(x);
481c⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲479b 483a ⊳
if A has with {0: %} then {
⟨exports: IndexedFreeAdditiveCombinationType: apply 482a⟩
}
481d⟨defaults: IndexedFreeAdditiveCombinationType 473b⟩+
≡ (465) ⊲479c 483b ⊳
if A has with {0: %} then {
⟨defaults: IndexedFreeAdditiveCombinationType: apply 482b⟩
}
Export of IndexedFreeAdditiveCombinationType
apply: (%, J) -> A
Description
Returns the coefficient corresponding to the given index.
An element f is a function f : J → A. The call apply(f,j) or f.j returns
f(j).
Remarks
If j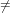 suppf then f(j) = 0.
suppf then f(j) = 0.
482a⟨exports: IndexedFreeAdditiveCombinationType: apply 482a⟩≡ (481c)
apply: (%, J) -> A;
482b⟨defaults: IndexedFreeAdditiveCombinationType: apply 482b⟩≡ (481d)
apply(x: %, j: J): A == {
import from I;
while not zero? x repeat {
(a, i) := leadingMonomial x;
x := reductum x;
c := compare(i, j);
zero? c => return a;
c < 0 => return 0;
}
0;
}
Uses I 47.
ToDo ⊲ 77 ⊳ rhx ⊲ 57 ⊳ 21-Jan-2007: This condition is questionable since we
require a function
zero? from
A. However, the availibility of a zero test does not
imply that the domain provides a general equality test. Therefore we implement
equality testing only if
A provides it.
483a⟨exports: IndexedFreeAdditiveCombinationType 468⟩+
≡ (465) ⊲481c 484a ⊳
if A has PrimitiveType then PrimitiveType;
483b⟨defaults: IndexedFreeAdditiveCombinationType 473b⟩+
≡ (465) ⊲481d 484b ⊳
if A has PrimitiveType then {
⟨defaults: IndexedFreeAdditiveCombinationType PrimitiveType 483c⟩
}
483c⟨defaults: IndexedFreeAdditiveCombinationType PrimitiveType 483c⟩≡ (483b)
(x: %) = (y: %): Boolean == {
import from A, J, I;
zero? x => zero? y;
zero? y => false;
(xa, xj) := leadingMonomial x;
(ya, yj) := leadingMonomial y;
xj ~= yj => false;
xa ~= ya => false;
reductum x = reductum y;
}
Uses I 47.
Let x and y be elements of the current domain then x < y if and only if one of the
following conditions holds.
- x = 0 ∧ y
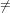 0
0
- x
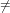 0 ∧ y
0 ∧ y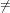 0 ∧ jx < jy
0 ∧ jx < jy
- x
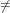 0 ∧ y
0 ∧ y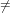 0 ∧ jx = jy ∧ x(jx) < y(jy)
0 ∧ jx = jy ∧ x(jx) < y(jy)
- x
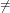 0 ∧ y
0 ∧ y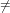 0 ∧ jx = jy ∧ x(jx) = y(jy) ∧ x′ < y′
0 ∧ jx = jy ∧ x(jx) = y(jy) ∧ x′ < y′
where jx = maxsupp(x) and x′ = reductum(x), and jy and y′ are defined analogously.
Note that this order has a minimal element, namely 0. This order is not additive
in general. Take A = J = ℤ and the functions a,b : ℤ → ℤ where a(0) = 1, b(0) = −1
and all other function value are zero. Then we clearly have 0 < a and 0 < b. However,
0 + a < a + b = 0 is false.
Nevertheless, the order is modelled after the lexicographic order starting the
comparison with the biggest index. It is sometimes also known as the reverse
lexicographical order (which should not be confused with the inverse lexicographical
order which is simply < −1 for the lexicographical order <, i. e., if a < b then
b < −1a).
485⟨defaults: IndexedFreeAdditiveCombinationType Order 485⟩≡ (484b) 486a ⊳
(x: %) < (y: %): Boolean == {import from I; compare(x, y) < 0}
Uses I 47.
Similarly, compare(x,y) is 0 if x = y, < 0 if x < y and > 0 if x > y.
486a⟨defaults: IndexedFreeAdditiveCombinationType Order 485⟩+
≡ (484b) ⊲485
compare(x: %, y: %): MachineInteger == {
import from A, J, I;
zero? x => if zero? y then 0 else -1;
zero? y => 1;
(xa, xj) := leadingMonomial x;
(ya, yj) := leadingMonomial y;
not zero?(c := compare(xj, yj)) => c;
not zero?(c := compare(xa, ya)) => c;
compare(reductum x, reductum y);
}
Uses I 47 and MachineInteger 67.
487⟨defaults: IndexedFreeAdditiveCombinationType OutputType 487⟩≡ (486c)
(tw: TextWriter) << (x: %): TextWriter == {
import from A, J, I, String;
tw := tw << "[";
while not zero? x repeat {
(xa, xj) := leadingMonomial x;
tw := tw << "(" << xa << "," << xj << ")";
x := reductum x;
}
tw << "]";
}
Uses I 47 and String 65.
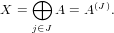
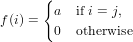
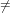 0 and 0 if
0 and 0 if 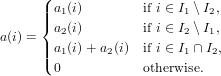
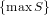 and
and 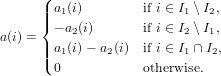
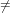 supp
supp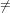 0
0
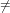 0
0 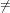 0
0 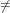 0
0 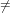 0
0 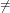 0
0 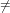 0
0