SparseFiniteMonoidRing

Convention ⊲ 4 ⊳

rhx ⊲ 60 ⊳ 26-Jan-2007: Categories corresponding to well established mathematical concepts like ring, group, etc., should be called like in mathematics. Domains implementing those concepts should be more specific about their implementation. For example, SparsePolynomial instead of just Polynomial.

Type Constructor

Description

Additive monoid of functions with finite support together with Cauchy product.

The domain constructor implements

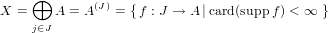X = ⊕ A = A(J) = {f : J → A |card(suppf) < ∞ }
j∈J

(179)

where A is known to be a ring and J is known to be a multiplicative semigroup.

Multiplication of A and J need not be commutative.

X is the monoid ring A[J] where elements of A commute with elements of J.

X will have a multiplicative unit if A has one and J is a monoid.

Parameters

A:: A ring.
J:: A totally ordered multiplicative monoid that serves as index set.

501⟨dom: SparseFiniteMonoidRing 501⟩≡   (462)
SparseFiniteMonoidRing(
    A: with {
            zero?: % -> Boolean;
            +: (%, %) -> %;
            *: (%, %) -> %
    },
    J: with {
            TotallyOrderedType;
            *: (%, %) -> %;
    }
): IndexedFreeArithmeticType(A, J) == SparseAdditiveArray(A, J) add {
        ⟨macros: FiniteMonoidRing 502a⟩
        Rep == SparseAdditiveArray(A, J);
        import from Rep;
        ⟨implementation: FiniteMonoidRing 502b⟩
}

Defines:
SparseFiniteMonoidRing, used in chunks 526 and 733.

Uses IndexedFreeArithmeticType 495, SparseAdditiveArray 489, and TotallyOrderedType 571.

502a⟨macros: FiniteMonoidRing 502a⟩≡ (501)
macro CAJ == Cross(A, J);

Defines:
CAJ, used in chunk 502b.

502b⟨implementation: FiniteMonoidRing 502b⟩≡   (501)  502c ⊳
local (aj: CAJ) * (bk: CAJ): CAJ == {
        import from A, J;
        (a, j) := aj;
        (b, k) := bk;
        (a*b, j*k)
}
(aj: CAJ) * (x: %): % == map((bk: CAJ): CAJ +-> aj*bk) x;
(x: %) * (y: %): % == {
        zero? x => x;
        zero? y => y;
        leadingMonomial x * y + reductum x * y;
}

Uses CAJ 502a.

502c⟨implementation: FiniteMonoidRing 502b⟩+≡ (501) ⊲502b 503b ⊳
if A has with {one?: % -> Boolean} and J has with {one?: % -> Boolean} then {
⟨implementation: FiniteMonoidRing: one? 503a⟩
}

503a⟨implementation: FiniteMonoidRing: one? 503a⟩≡   (502c)
one?(x: %): Boolean == {
        import from A, J;
        zero? x or not zero? reductum x => false;
        (xa, xj) := leadingMonomial x;
        one? xa and one? xj;
}

503b⟨implementation: FiniteMonoidRing 502b⟩+≡ (501) ⊲502c 503d ⊳
if A has with {1: %} and J has with {1: %} then {
1: % == [1$A, 1$J];
}

503c⟨exports: FiniteMonoidRing 503c⟩≡
if A has OutputType and J has OutputType then OutputType;

Uses OutputType 570.

503d⟨implementation: FiniteMonoidRing 502b⟩+≡ (501) ⊲503b
if A has OutputType and J has OutputType then {
⟨implementation: FiniteMonoidRing output 504⟩
}

Uses OutputType 570.

504⟨implementation: FiniteMonoidRing output 504⟩≡   (503d)
#if Axiom
local term(a: A, j: J): OutputForm == {
        if A has with { OutputType; one?: % -> Boolean }
        then {
                if one? a
                then tw := j::OutputForm
                else tw := a::OutputForm * j::OutputForm;
        }
        else tw := a::OutputForm * j::OutputForm;
}
coerce(x: %): OutputForm == {
        import from A, J, String, Boolean;
        zero? x => message "0";
        (a, j) := leadingMonomial x;
        x := reductum x;
        tw := term(a, j);
        while not zero? x repeat {
                (a, j) := leadingMonomial x;
                tw := tw + term(a, j);
                x := reductum x;
        }
        tw;
}
#endif
(tw: TextWriter) << (x: %): TextWriter == {
        import from A, J, String;
        zero? x => tw << "0";
        (a, j) := leadingMonomial x;
        x := reductum x;
        tw := tw << "(" << a << ")*" << j;
        while not zero? x repeat {
                (a, j) := leadingMonomial x;
                tw := tw << "+(" << a << ")*" << j;
                x := reductum x;
        }
        tw;
}

Uses OutputType 570 and String 65.

17.4 SparseFiniteMonoidRing