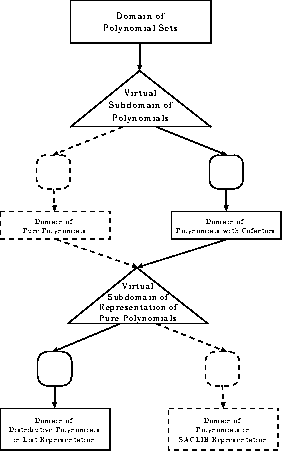
Figure: 2-level Structure of Polynomials
Polynomials receive our special attention. We formulate the Gröbner bases algorithm for ``sets of polynomials'', hence, the term ``polynomial'' must be kept rather general: it may be a polynomial in the strict mathematical sense (a ``pure polynomial'') but it may as well be a pure polynomial with some additional information attached, which allows further interpretation of the result. This additional information could for instance be the cofactors with respect to the initial polynomials. Computing a Gröbner basis for a set of ``polynomials with cofactors'' (see Section 3.13) yields a Gröbner basis plus a representation of each basis polynomial in terms of the initial polynomials.
Independent of this structure , we can choose among different representations for ``pure polynomials'' , for instance the distributive list representation (see Section 3.12) or the various representations provided by SACLIB. Whatever structure is used for ``polynomials'', the representation of a ``pure polynomial'' will occur as a virtual subdomain.
Thus, the domain ``polynomials'' as a virtual subdomain of ``sets of polynomials'' should have the 2-level structure as shown in Figure 5.

Figure: 2-level Structure of Polynomials