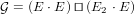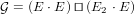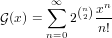29.2 Test Functorial Composition
Simple graphs can be described by as a functorial composite of subsets ℘ = E ⋅E
and subsets of 2-element sets ℘[2] = E2 ⋅ E,
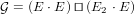 |
(193)
|
where E is the species of sets and E2 the species of 2-element sets, see [BLL98,
Chp. 2.2]. The exponential generating series of G is given in Example 1.2.2 of
[BLL98]. 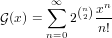 |
(194)
|
706⟨test series 686a⟩+
≡ (685 704) ⊲705
testFunctorialCompose1(): () == {
macro S == ExponentialGeneratingSeries;
import from S, Q, DataStream Q;
e: S := stream(inv(fn) for fn in factorialStream) :: S;
e2: S := term(inv 2, 2);
h: S := functorialCompose(e * e, e2 * e);
l1: List Z := [2^(binomial(n,2)$MultinomialTools) for n:I in 0..9];
l2: List Z := [count(h, n) for n:I in 0..9];
assertEquals(List Z, l1, l2);
}
Uses DataStream 386, ExponentialGeneratingSeries 316, I 47, MultinomialTools 367,
Q 47, and Z 47.
The values for the cycle indicator series are taken from [BLL98, Appendix 2,
Table 6].
ToDo ⊲ 90 ⊳ The test currently fails. It seems that the computation of the
cycleindicatorseries forgets about variables other than
x1. This makes the
corresponding test in
src/species.as.nw fail, too - raising an exception since the
sum of the coefficients is not an integer.
707⟨test polynomial series 707⟩≡ (704) 710 ⊳
testFunctorialCompose2(): () == {
macro {
V == CycleIndexVariable;
T == SparseIndexedPowerProduct(V, I);
P == SparseDistributedPolynomial(Q, V, T);
S == CycleIndexSeries;
}
import from S, I, Z, Q, V, T, P, DataStream P;
local x(i: I, e: I): P == power(i :: V, e) :: P;
import from S, Q, DataStream Q;
e: S := cycleIndexSeries $ SetSpecies(Z);
e2: S := term(coefficient(e, 2), 2);
h: S := functorialCompose(e * e, e2 * e);
l1: List P := [
1,
x(1,1),
x(1,2)+x(2,1),
(4/3)*x(1,3)+2/1*x(1,1)*x(2,1)+2/3*x(3,1),
(8/3)*x(1,4)+4/1*x(1,2)*x(2,1)+4/3*x(1,1)*x(3,1)
+2/1*x(2,2)+x(4,1),
128/15*x(1,5)+32/3*x(1,3)*x(2,1)+8/3*x(1,2)*x(3,1)
+2/1*x(1,1)*x(4,1)+8/1*x(1,1)*x(2,2)+4/3*x(2,1)*x(3,1)
+4/5*x(5,1),
2048/45*x(1,6)+128/3*x(1,4)*x(2,1)+64/9*x(1,3)*x(3,1)
+4/1*x(1,2)*x(4,1)+8/5*x(1,1)*x(5,1)+32/3*x(2,3)
+32/1*x(1,2)*x(2,2)+16/9*x(3,2)+16/3*x(1,1)*x(2,1)*x(3,1)
+4/1*x(2,1)*x(4,1)+4/3*x(6,1)
];
l2: List P := [q for p in l1 for q in coefficients h];
assertEquals(List P, l1, l2);
}
Uses CycleIndexSeries 330, CycleIndexVariable 329, DataStream 386, I 47, Q 47,
SetSpecies 117, SparseDistributedPolynomial 526, SparseIndexedPowerProduct 506,
and Z 47.