


Nächste Seite: Variationsrechnung
Aufwärts: Sätze und Definitionen
Vorherige Seite: Zyklen von Kontinuierlichen Systemen
Wenn
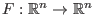 ein stetiges Richtungsfeld ist, und
ein stetiges Richtungsfeld ist, und
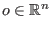 kein Gleichgewichtspunkt
ist, dann ist der Fluß von
kein Gleichgewichtspunkt
ist, dann ist der Fluß von 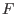 lokal equivalent zum Fluß eines konstanten
Vektorfelds. Wenn nun das Richtungsfeld von einem oder mehreren reellen Parametern
abhängt und diese Parameter Störungen unterliegen, dann ändert sich das lokale
Verhalten qualitativ nicht, solange die Störung klein genug ist (solange nur das Richtungsfeld
bei
lokal equivalent zum Fluß eines konstanten
Vektorfelds. Wenn nun das Richtungsfeld von einem oder mehreren reellen Parametern
abhängt und diese Parameter Störungen unterliegen, dann ändert sich das lokale
Verhalten qualitativ nicht, solange die Störung klein genug ist (solange nur das Richtungsfeld
bei 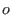 nicht verschwindet).
nicht verschwindet).
Auch wenn 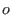 ein hyperbolischer Gleichgewichtspunkten ist, ist das lokale Verhalten
unabhängig von kleinen Störungen. Das besagt der folgende Satz.
ein hyperbolischer Gleichgewichtspunkten ist, ist das lokale Verhalten
unabhängig von kleinen Störungen. Das besagt der folgende Satz.
Satz 23
Es sei
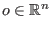 ,
,
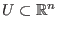 eine offene Umgebung von
eine offene Umgebung von 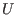 ,
,
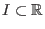 ein Intervall,
welches 0
als inneren Punkt enthält,
ein Intervall,
welches 0
als inneren Punkt enthält,
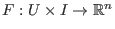 ein Richtungsfeld, sodaß
ein Richtungsfeld, sodaß
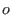 ein hyperbolischer Gleichgewichtspunkt des Richtungsfeldes bei 0
ist. Dann gibt es
ein Teilintervall
ein hyperbolischer Gleichgewichtspunkt des Richtungsfeldes bei 0
ist. Dann gibt es
ein Teilintervall
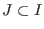 , sodaß für alle
, sodaß für alle
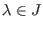 das Richtungsfeld bei
das Richtungsfeld bei
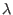 wieder einen hyperbolischen Gleichgewichtspunkt besitzt. Dabei ist das qualitative
Verhalten gleich dem des Gleichgewichtsounktes
wieder einen hyperbolischen Gleichgewichtspunkt besitzt. Dabei ist das qualitative
Verhalten gleich dem des Gleichgewichtsounktes 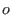 im Richtungsfeldes bei 0
.
im Richtungsfeldes bei 0
.
Beweis.
Für
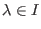
bezeichnen wir mit
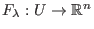
,
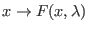
das
Richtungsfeld bei
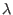
. Die Funktion
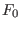
bildet den Punkt
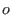
auf den Nullpunkt ab
und hat Jacobi-determinante ungleich 0 (da alle Eigenwerte Reilteil ungleich Null haben).
Nach dem Satz über implizite Funktionen ist
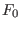
ein lokaler Isomorphismus von einer
eventuell kleineren Umgebung
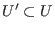
auf eine Umgebung
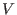
des Nullpunkts. Das
Nicht-Verschwinden der Jacobi-determinante ist auch noch erfüllt für
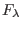
, falls
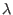
nahe genug bei Null ist. Nach eventueller weiterer Verkleinerung der Umgebungen
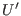
und
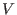
ist
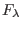
ein Isomorphismus von
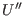
und
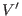
, und das inverse Bild
des Nullpunkts ist der einzige Gleichgewichtspunkt von
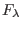
in
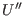
. Die Stetigkeit
der Eigenwerte liefert den Rest der Behauptung.

Im Gegensatz dazu können nichthyperbolische Gleichgewichtspunkte durch kleine Störungen
den Typ ändern, verschwinden, oder in mehrere Gleichgewichtspunkte ``aufspalten''. In der
Bifurkationstheorie werden die Möglichkeiten untersucht, wie nichthyperbolische Gleichgewichtspunkte
durch kleine Störungen beeinflußt werden.
- Sattelknoten-Bifurkation:
-
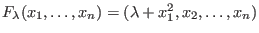 .
Für
.
Für 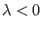 befinden sich in der Nähe von
befinden sich in der Nähe von
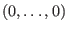 eine Quelle und ein
Sattelpunkt (bzw. Senke falls
eine Quelle und ein
Sattelpunkt (bzw. Senke falls 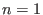 ), für
), für 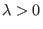 gibt es keine Equilibrien.
gibt es keine Equilibrien.
- transkritische Bifurkation:
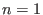 ,
,
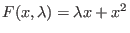 . Hier gibt es für
. Hier gibt es für
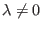 zwei Equilibrien, eine Quelle und eine Senke, die beim Durchgang durch
Null ``den Typ vertauschen''.
zwei Equilibrien, eine Quelle und eine Senke, die beim Durchgang durch
Null ``den Typ vertauschen''.
Graphische Darstellung von Bifurkationsdiagrammen im Fall 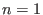 : In der
: In der
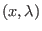 -Ebene
werden für jedes
-Ebene
werden für jedes 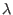 die hyperbolischen Gleichgewichtspunkte durch Kurven gezeichnet,
wobei Senken als durchgehende Kurven und Quellen strichliert dargestellt werden.
die hyperbolischen Gleichgewichtspunkte durch Kurven gezeichnet,
wobei Senken als durchgehende Kurven und Quellen strichliert dargestellt werden.
Definition 19
Es sei
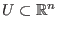
offen. Es sei
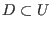
eine kompakte Teilmenge von
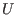
mit glattem Rand.
Ein stetig differenzierbares Vektorfeld
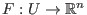
heißt
strukturell stabil auf
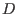
, wenn
es zu jedem ein-parametrigem differenzierbarem Vektorfeld
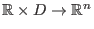
,
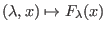
ein
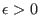
gibt, sodaß
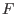
auf
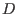
topologisch äquivalent
ist zu
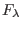
für alle
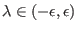
. Das heißt, es existiert ein
Homöomorphimus von
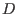
nach
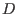
, der Orbits von
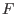
in Orbits von
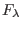
abbildet und
die Pfeilrichtungen erhält.
Satz 24
Im Fall 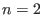 ist ein differenzierbares Vektorfeld genau dann stabil, wenn alle seine Gleichgewichtspunkte
und Zyklern hyperbolisch sind, und wenn keine homoklinen oder heteroklinen Orbits existieren.
ist ein differenzierbares Vektorfeld genau dann stabil, wenn alle seine Gleichgewichtspunkte
und Zyklern hyperbolisch sind, und wenn keine homoklinen oder heteroklinen Orbits existieren.
- Literatur:
- [2, I.2,III.13.1]



Nächste Seite: Variationsrechnung
Aufwärts: Sätze und Definitionen
Vorherige Seite: Zyklen von Kontinuierlichen Systemen
Josef Schicho
2016-01-17
![]() ein stetiges Richtungsfeld ist, und
ein stetiges Richtungsfeld ist, und
![]() kein Gleichgewichtspunkt
ist, dann ist der Fluß von
kein Gleichgewichtspunkt
ist, dann ist der Fluß von ![]() lokal equivalent zum Fluß eines konstanten
Vektorfelds. Wenn nun das Richtungsfeld von einem oder mehreren reellen Parametern
abhängt und diese Parameter Störungen unterliegen, dann ändert sich das lokale
Verhalten qualitativ nicht, solange die Störung klein genug ist (solange nur das Richtungsfeld
bei
lokal equivalent zum Fluß eines konstanten
Vektorfelds. Wenn nun das Richtungsfeld von einem oder mehreren reellen Parametern
abhängt und diese Parameter Störungen unterliegen, dann ändert sich das lokale
Verhalten qualitativ nicht, solange die Störung klein genug ist (solange nur das Richtungsfeld
bei ![]() nicht verschwindet).
nicht verschwindet).
![]() ein hyperbolischer Gleichgewichtspunkten ist, ist das lokale Verhalten
unabhängig von kleinen Störungen. Das besagt der folgende Satz.
ein hyperbolischer Gleichgewichtspunkten ist, ist das lokale Verhalten
unabhängig von kleinen Störungen. Das besagt der folgende Satz.
![]() : In der
: In der
![]() -Ebene
werden für jedes
-Ebene
werden für jedes ![]() die hyperbolischen Gleichgewichtspunkte durch Kurven gezeichnet,
wobei Senken als durchgehende Kurven und Quellen strichliert dargestellt werden.
die hyperbolischen Gleichgewichtspunkte durch Kurven gezeichnet,
wobei Senken als durchgehende Kurven und Quellen strichliert dargestellt werden.