


Nächste Seite: Zyklen von Diskreten Dynamischen
Aufwärts: Sätze und Definitionen
Vorherige Seite: Der Fluß eines Vektorfeld
Es sei
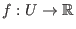 eine differenzierbare Funktion. Dann ist die Richtungsableitung
definiert als
eine differenzierbare Funktion. Dann ist die Richtungsableitung
definiert als
Wenn
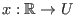 eine Lösungskurve ist, dann ist
eine Lösungskurve ist, dann ist
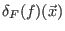 die Ableitung
der Funktion
die Ableitung
der Funktion
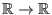 ,
,
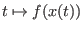 .
.
Bei Gleichgewichtspunkten ist die Richtungsableitung jeder Funktion gleich Null. Eine Funktion 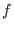 ist also dann strikt Ljapunov beim Gleichgewichtspunkt
ist also dann strikt Ljapunov beim Gleichgewichtspunkt 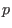 , wenn
, wenn 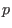 gleichzeitig lokales Maximum von
gleichzeitig lokales Maximum von 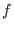 und lokales Minimum von
und lokales Minimum von
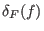 ist.
ist.
Beweis.
Die Lösungskurven können die Teilgebiete
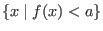
, wobei
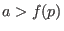
ist,
nie verlassen. Außerdem ist die Ableitung der Funktion
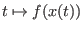
stets
negativ für
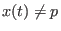
, daher ist
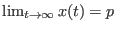
für alle Lösungskurven.

Satz 16
Es sei 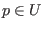 ein Equilibrium, sodaß die Eigenwerte der Jacobi-Matrix bei
ein Equilibrium, sodaß die Eigenwerte der Jacobi-Matrix bei 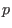
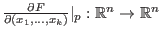 alle positiven bzw. negativen Realteil haben.
Dann ist
alle positiven bzw. negativen Realteil haben.
Dann ist 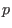 asymptotisch stabil.
asymptotisch stabil.
Definition 14
Ein Gleichgewichtspunkt, bei dem die Eigenwerte der Jacobi-Matrix Realteil ungleich Null
haben, heißt hyperbolischer Gleichgewichtspunkt.
Definition 15
Eine
Senke ist ein asymptotisch stabiler Gleichgewichtspunkt.
Eine
Quelle ist ein instabiler Gleichgewichtspunkt, der bei der Multiplikation des Richtungsfelds
mit
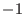
asymptotisch stabil wird.
Ein
Sattelpunkt ist ein hyperbolischer Gleichgewichtspunkt, der weder eine Quelle noch eine Senke ist.
Im Fall 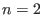 sind alle Sattelpunkte lokal äquivalent. Für jeden Sattelpunkt gibt es 4 ausgezeichnete
Orbits, zwei ``hineingehende'' und zwei ``hinausgehende'' Orbits.
sind alle Sattelpunkte lokal äquivalent. Für jeden Sattelpunkt gibt es 4 ausgezeichnete
Orbits, zwei ``hineingehende'' und zwei ``hinausgehende'' Orbits.
- Literatur:
- [2, III.8.3,III.9.1,III.9.3]



Nächste Seite: Zyklen von Diskreten Dynamischen
Aufwärts: Sätze und Definitionen
Vorherige Seite: Der Fluß eines Vektorfeld
Josef Schicho
2016-01-17
![]() eine differenzierbare Funktion. Dann ist die Richtungsableitung
definiert als
eine differenzierbare Funktion. Dann ist die Richtungsableitung
definiert als
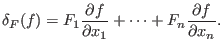
![]() ist also dann strikt Ljapunov beim Gleichgewichtspunkt
ist also dann strikt Ljapunov beim Gleichgewichtspunkt ![]() , wenn
, wenn ![]() gleichzeitig lokales Maximum von
gleichzeitig lokales Maximum von ![]() und lokales Minimum von
und lokales Minimum von
![]() ist.
ist.
![]() die Anzahl der Eigenwerte der Jacobimatrix von
die Anzahl der Eigenwerte der Jacobimatrix von
![]() mit positivem Realteil.
Wenn
mit positivem Realteil.
Wenn ![]() ist, dann ist
ist, dann ist ![]() eine Senke; wenn
eine Senke; wenn ![]() ist, ist
ist, ist ![]() eine Quelle; in allen anderen Fällen
ist
eine Quelle; in allen anderen Fällen
ist ![]() ein Sattelpunkt.
ein Sattelpunkt.![]() sind alle Sattelpunkte lokal äquivalent. Für jeden Sattelpunkt gibt es 4 ausgezeichnete
Orbits, zwei ``hineingehende'' und zwei ``hinausgehende'' Orbits.
sind alle Sattelpunkte lokal äquivalent. Für jeden Sattelpunkt gibt es 4 ausgezeichnete
Orbits, zwei ``hineingehende'' und zwei ``hinausgehende'' Orbits.