


Nächste Seite: Lineare Rekursionen mit konstanten
Aufwärts: Sätze und Definitionen
Vorherige Seite: Gleichgewichtspunkte und Stabilität (Definition)
Die allgemeine Gestalt der skalaren linearen Differentialgleichung von Ordnung 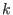 ist
ist
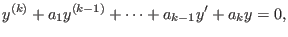 |
(1) |
wobei
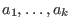 reelle oder komplexe Konstanten sind, und
reelle oder komplexe Konstanten sind, und
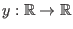 bzw.
bzw.
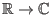 die
unbestimmte Funktion ist. (Die obige Gleichung ist als Gleichheit von Funktionen zu verstehen,
auf der rechten Seite steht die Nullfunktion
die
unbestimmte Funktion ist. (Die obige Gleichung ist als Gleichheit von Funktionen zu verstehen,
auf der rechten Seite steht die Nullfunktion
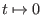 .) Wir behandeln in erster Linie den reellen Fall.
.) Wir behandeln in erster Linie den reellen Fall.
Wir bezeichnen die Menge aller beliebig oft differenzierbaren Definitionen von
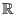 nach
nach
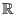 mit
mit
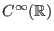 .
Die linke Seite von (3) läßt sich schreiben als
.
Die linke Seite von (3) läßt sich schreiben als 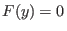 , wobei
, wobei
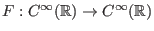 der Operator
der Operator
ist.
Das charakteristische Polynom von (3) ist
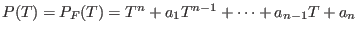 .
.
Satz 5
Es seien 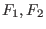 lineare Differentialoperatoren mit konstanten Koeffizienten.
Dann ist
lineare Differentialoperatoren mit konstanten Koeffizienten.
Dann ist
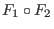 wieder linearer Differentialoperator mit konstanten Koeffizienten.
Es gilt
wieder linearer Differentialoperator mit konstanten Koeffizienten.
Es gilt
Satz 6
Es sei 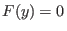 eine lineare Differentialgleichung
eine lineare Differentialgleichung 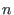 -ter Ordnung mit konstanten Koeffizienten.
Es sei
-ter Ordnung mit konstanten Koeffizienten.
Es sei
die Zerlegung vom charakteristischen Polynom in komplexe Linearfaktoren.
Dann sind die Lösungen von 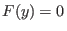 genau die Linearkombinationen der Lösungen
genau die Linearkombinationen der Lösungen
Insbesondere bilden die Lösungen einen Vektorraum der Dimension 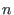 .
.
Im reellen Fall erhält man durch den obigen Satz nur eine Basis von komplexwertigen
Lösungen. Diese lassen sich aber mit Hilfe der Eulerschen Formeln durch reelle Basislösungen
ersetzen. Zum Beispiel erzeugen die Funktionen
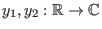 ,
,
über
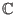 den selben Vektorraum wie die Funktionen
den selben Vektorraum wie die Funktionen
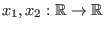
Die Funktionen 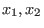 sind jedoch reellwertig und erzeugen über
sind jedoch reellwertig und erzeugen über
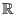 alle reellwertigen
Lösungen.
alle reellwertigen
Lösungen.
Beim Anfangswertproblem sind zusätzlich zur Gleichung 3 die Anfangsbedingungen
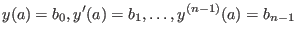 |
(2) |
vorgegeben, wobei
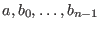 gegebene reelle oder komplexe Zahlen sind.
gegebene reelle oder komplexe Zahlen sind.
Satz 7
Das Anfangswertproblem 3,2 besitzt eine eindeutige Lösung.
Wenn
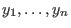 eine Basis des Lösungsraumes ist, dann ist die Wronskische Determinante
eine Basis des Lösungsraumes ist, dann ist die Wronskische Determinante
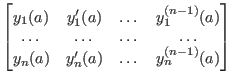 ungleich 0.
ungleich 0.
- Literatur:
- [3, IV.15]



Nächste Seite: Lineare Rekursionen mit konstanten
Aufwärts: Sätze und Definitionen
Vorherige Seite: Gleichgewichtspunkte und Stabilität (Definition)
Josef Schicho
2016-01-17
![]() ist
ist
![]() nach
nach
![]() mit
mit
![]() .
Die linke Seite von (3) läßt sich schreiben als
.
Die linke Seite von (3) läßt sich schreiben als ![]() , wobei
, wobei
![]() der Operator
der Operator
![]() ,
,
![]() eine Basis des Lösungsraumes ist, dann ist die Wronskische Determinante
eine Basis des Lösungsraumes ist, dann ist die Wronskische Determinante
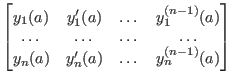 ungleich 0.
ungleich 0.