Existenz und Eindeutigkeit

Ein metrischer Raum $X$ mit Metrik $d:X\times X\to\mathbb{R}$ heißt vollständig, wenn jede Cauchy-Folge in $X$ einen Grenzwert in $X$ hat.

Es sei $D\subset\mathbb{R}$ ein (offenes oder geschlossenes, beschränktes oder unbeschränktes) Intervall. Es sei $C^0_b(D,\mathbb{R}^k)$ die Menge der stetigen und beschränkten Funktionen von $D$ nach $\mathbb{R}^k$ .

Satz 9   Die Menge $C^0_b(D,\mathbb{R}^k)$ ist bezüglich der Norm $(f,g)\mapsto\sup_{x\in D}\vert\vert f(x)-g(x)\vert\vert$ stetig, wobei $\vert\vert\cdot \vert\vert$ die Euklidische Norm auf $\mathbb{R}^k$ ist.

Beweis. Es sei $(f_n)_n$ eine Cauchy-Folge von stetigen Funktionen. Für jedes $x$ ist dann auch die Folge der Funktionswerte $(f_n(x))_n$ Cauchy, weil $\vert f_m(x)-f_m(x)\vert\le d(f_m,f_n)$ gilt. Die reellen Zahlen sind vollständig, daher existiert der Grenzwert und wir können die Grenzfunktion $\bar{f}:D\to\mathbb{R}$ definieren durch $\bar{f}(x)=\lim_{n\to\infty}f_n(x)$ .

Um zu zeigen daß $\bar{f}$ stetig ist, wählen wir $\epsilon>0$ und $n$ so, daß $d(f_n,\bar{f})<\epsilon/3$ ist. Wir wählen auch ein kompaktes Teilintervall $I\subset D$ , in diesem ist $f_n$ gleichmäßig stetig und es existiert $\delta$ mit $\vert f_n(x)-f_n(y)\vert\le\epsilon/3$ . Dann ist wegen der Dreiecksungleichung $\vert\bar{f}(x)-\bar{f}(y)\vert\le \vert\bar{f}(x)-f_n(x)\vert+\vert f_n(x)-f_n(y)\vert+\vert f_n(y)-\bar{f}(y)\vert <\epsilon/3+\epsilon/3+\epsilon/3=\epsilon$ für alle $x,y\in I$ mit $\vert x-y\vert<\delta$ , also ist $\bar{f}$ gleichmäßig stetig in $I$ . Das gilt für jedes kompakte Teilintervall, daher ist $\bar{f}$ in ganz $D$ stetig. $\qedsymbol$

Satz 10 (Banachscher Fixpunktsatz)   Es sei $X$ ein vollständiger metrischer Raum und $f:X\to X$ eine kontrahierende Abbildung, das heißt es existiert $c<1$ sodaß für alle $x,y\in X$ gilt $d(f(x),f(y))\le cd(x,y)$ . Dann besitzt $f$ einen eindeutigen Fixpunkt.

Satz 11 (Picard/Lindelöf)   Es sei $D$ ein Intervall (offen oder abgeschlossen, beschränkt oder unbeschränkt), $k$ eine positive ganze Zahl, $F:D\times\mathbb{R}^k\to\mathbb{R}^k$ eine stetige Funktion, die die Lipschitz-Bedingung erfüllt: es existiert eine Konstante $L\in\mathbb{R}$ , sodaß für alle $x\in D, y,z\in\mathbb{R}^k$ gilt $\vert\vert F(x,y)-F(x,z)\vert\vert\le L\vert\vert y-z\vert\vert$ . Es sei $x_0\in D$ , $y_0\in\mathbb{R}^k$ . Dann hat das Anfangswertproblem

$$y'(x)=F(x,y(x)), \ y(x_0)=y_0$$

eine eindeutige Lösung $y:D\to\mathbb{R}^k$ .

Beweis. Wir beweisen den Satz zunächst für ein kompaktes Teilintervall $I=[a,b]$ in $D$ . Wir definieren den Operator $P:C^0_b(I)\to C^0_b(I)$ durch

$$f \mapsto P(f), P(f)(x)=y_0+\int_{x_0}^x F(t,f(t))dt$$

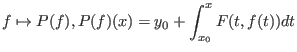
Jede Lösung des Anfangwertproblems ist ein Fixpunkt von $P$ , und umgekehrt ist jeder Fixpunkt differenzierbar und löst das Anfangswertproblem. Durch Abschätzen des Integrals zeigt man die Ungleichung

$$d(P(f),P(g)) \le L(b-a) d(f,g)$$

für alle $f,g\in C^0_b(I)$ .

Falls $L(b-a)<1$ ist, gilt die Existenz und Eindeutigkeit wegen Satz 10. Im allgemeinen Fall, bzw. falls $D$ nicht kompakt ist, kann man $D$ überdecken durch überlappende kompakte Teilintervalle und bekommt die Existenz und Eindeutigkeit durch Fortsetzen der Lösung auf den Teilintervallen. $\qedsymbol$

Der Satz von Picard/Lindelöf gilt auch für Differentialgleichungen höherer Ordnung, weil diese durch Einführung von Geschwindigkeitskoordinaten auf vektorielle Differentialgleichungen zurückgeführt werden können. Hier sind auch die Werte der Ableitungen bis zur Ordnung minus 1 an der Anfangsstelle vorzugeben.

Literatur:

[3, III.12, IX.60]