


Nächste Seite: Rückführung auf Systeme erster
Aufwärts: Sätze und Definitionen
Vorherige Seite: Sätze und Definitionen
Definition 1
Ein dynamisches System ist eine Beschreibung von Funktionen in einer reellen (kontinuierliches System) oder
natürlichen (diskretes System) Variablen durch Differentialgleichungen (im kontinuierlichen Fall) oder
Rekursionsgleichungen (im diekreten Fall). Charakteristisch für die Beschreibung ist, daß das Verhalten
der Funktionen, die durch diese Gleichung beschrieben ist, eindeutig von ihrem Wert an einer Anfangsstelle
bestimmt ist (deterministisches System).
Definition 3
Die Ordnung einer gewöhnlichen Differentialgleichung ist die höchste Ordung
der Ableitung der unbestimmten Funktion, die in der Gleichung vorkommt.
Definition 4
Eine Differentialgleichung heißt linear, wenn sie sich schreiben läßt als
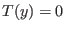
, wobei
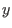
die gesuchte Funktion und
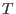
ein linearer Differentialoperator ist.
Ein linearer Differentialoperator ist rekursiv definiert als
- der identische Operator
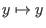 ,
,
- der Ableitungsoperator
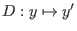 ,
,
- die Summe zweier Differentialoperatoren,
- die Hintereinanderausführung zweier Differentialoperatoren,
- oder das Produkt eines Differentialoperators mit einer bestimmten Funktion.
Satz 1
Die Lösungen einer linearen Differentialgleichungen bilden einen Vektorraum, m.a.W.
die Lösungsmenge ist abgeschlossen bezüglich Addition und Multiplikation mit
Konstanten.
Eine Differentialgleichung heißt autonom oder zeitunabhängig, wenn jede
innerste Funktion entweder die gesuchte Funktion oder eine ihrer Ableitungen ist, so wie in
Die allgemeine Form der vektorwertigen autonomen Differentialgleichung erster Ordnung für eine Funktion
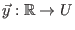 , wobei
, wobei
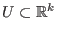 und
und 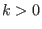 , ist
, ist
wobei
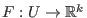 eine stetige Funktion ist. Diese Funktion wird auch als Vektorfeld
oder Richtungsfeld bezeichnet.
eine stetige Funktion ist. Diese Funktion wird auch als Vektorfeld
oder Richtungsfeld bezeichnet.
Definition 5
Die obigen Begriffe (Ordnung, Linearität) sind in abgewandelter Form auch für Rekursionsgleichungen gültig.
Bei Rekursionsgleichung wird der Funktionswert an einer Stelle
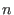
gleichgesetzt mit einem Ausdruck
in Funktionswerten an Stellen kleiner als
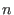
. Wenn die kleinste dieser Stellen
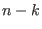
ist, dann
heißt
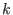
die Ordnung der Rekursionsgleichung.



Nächste Seite: Rückführung auf Systeme erster
Aufwärts: Sätze und Definitionen
Vorherige Seite: Sätze und Definitionen
Josef Schicho
2016-01-17
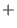 ,
, 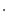 ,
, 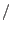 );
);
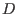 (bei partiellen Differentialgleichungen: partielle Ableitungen);
(bei partiellen Differentialgleichungen: partielle Ableitungen);
![]() , wobei
, wobei
![]() und
und ![]() , ist
, ist