7.1.3 Another Construction of Number Domains
Integer Numbers
We have introduced in Section The Integer Numbers an integer
as a pair <x, y> of natural numbers x and y
such that their difference denotes the desired value. In order to
determine this pair uniquely, either x or y has been chosen
zero; we are now going to lift this artificial restriction by defining an
integer as the class of all pairs with the same difference.
Definition 109 (Integer Numbers)
|
x ~ Z y : <=> (x0 +N y1 =
y0 +N x1) |
|
|
|
Z:= (N x N)/ ~ Z |
|
|
|
0 := [<0N, 0N>]; 1 := [<1N, 0N>]; 2 := [<2N, 0N>] |
|
|
|
x := such a in N x N: x = [a]
|
|
x + y | := | [<x0+Ny0,x1+Ny1>] |
|
- x | := | [<x1,x0>] |
|
x - y | := | [<x0+Ny1,y0+Nx1>] |
|
x * y | := |
[<(x0*Ny0)+N(x1*Ny1),
(x0*Ny1)+N(x1*Ny0)>] |
|
x <= y | : <=> |
x0+y1 <= N y0+x1 |
|
|
In above definition, [x] denotes [x] ~ Z.
It is easy to see that ~ Z is an equivalence relation, therefore
Z is a partition of N x N. The corresponding equivalence
classes satisfy congruence properties similar to those of
Proposition Congruence Properties such that the
results of all operations are uniquely defined.
Example
|
5 | = | [<7,2>] = {<5, 0>, <6, 1>, <7, 2>,
<8, 3>, ...} |
|
-6 | = | [<3,9>] =
{<0, 6>, <1, 7>, <2, 8>, <3, 9>, ...} |
|
5+(-6) | = | [<7,2>] + [<3,9>] = [<10, 11>] = [<0,
1>] = -1 |
|
5*(-6) | = | [<7,2>] * [<3,9>] = [<39, 69>] = [<0,
30>] = -30 |
|
5 <= -6 | <=> | [<7,2>] <= [<3,9>] <=> 16 <= 5
<=> F.
|
The new construction is isomorphic to the old one such that
the properties of all operations are preserved.
Proposition 124 (Isomorphism of Integer Constructions)
Let Z' denote the old construction of the integers and Z
denote the new one. The function
is an isomorphism with respect to 0, +, -, *, <, i.e., i is bijective
and for all x in Z' and y in Z', we have:
|
i(0Z') | = | 0Z, |
|
i(x+Z'y) | = | x+Zy, |
|
i(-Z' x) | = | -Z x, |
|
i(x-Z'y) | = | x-Zy, |
|
i(x*Z'y) | = | x*Zy, |
|
x <= Z' y | <=> | i(x) <= Z
i(y).
|
It is easy to see that the inverse isomorphism is denoted by
where "I" denotes the constructor function on Z'.
Proof
Take arbitrary x in Z' and y in Z'.
We prove
We know
|
i(x+Z'y) | = |
i(I(x0 +N y0,
x1 +N y1)).
|
- Case x0 +N y0 >= x1 +N y1:
-
We have
|
i(I(x0 +N y0,
x1 +N y1)) | = | |
|
i(<(x0 +N y0) -
(x1 +N y1)>) | = | |
|
[<(x0 +N y0) -
(x1 +N y1)>] | = | (definition ~ Z) |
|
[<x0 +N y0,
x1 +N y1>] | = | |
|
x +Z y.
|
- Case x0 +N y0 <
x1 +N y1:
-
Proceeds analogously.
An implementation of this construction in the Logic Evaluator is shown below,
see Appendix integer2.txt.
Rational Numbers
In Section The Rational Numbers, we have defined a rational
as a pair <x, y> of integer numbers x and
y such that their quotient denotes the desired value. In order
to determine this pair uniquely, x and y have been chosen
relatively prime with y being positive. We will now lift this
restriction by defining a rational as the class of all pairs with the same
quotient.
Definition 110 (Rational Numbers)
|
x ~ Q y : <=> (x0 *Z y1 =
y0 *Z x1) |
|
|
|
Q:= (Z x Z != 0)/ ~ Q |
|
|
|
0 := [<0Z, 1Z>];
1 := [<1Z, 1Z>];
2 := [<2Z, 1Z>];
|
|
|
|
x := such a in Z x Z: x =
[a]
|
|
x + y | := | [<(x0 *Z
y1) +Z
(y0 *Z x1),
x1 *Z y1>] |
|
- x | := | [<-Z x0,
x1>] |
|
x - y | := | [<(x0 *Z
y1) -Z
(y0 *Z x1),
x1 *Z y1>] |
|
x * y | := | [<x0 *Z
y0,
x1 *Z y1>] |
|
x-1 | := | [<x1, x0>]
|
|
x/y | := | [<x0 *Z
y1, y0 *Z
x1>] |
|
x <= y | : <=> |
x0 *Z y1 <= Z
y0 *Z x1
|
It is easy to see that ~ Q is an equivalence relation on Z x Z != 0 where Z != 0 := {x in Z: x != 0}; we have a corresponding partition that also
satisfies the necessary congruence properties such that the results of all
operations are uniquely defined.
Example
|
4/6 | = | [<4, 6>] = {<2, 3>, <-2, -3>,
<4, 6>, <-4, -6>, <6, 9>, ...} |
|
-2/5 | = | -[<2, 5>] =
[<-2, 5>] |
|
| = | {<2, -5>, <-2, 5>,
<4, -10>, <-4, 10>, <6, -15>, ...}
|
|
4/6 + (-2/5) | = | [<4, 6>] + [<-2, 5>] =
[<8, 30>] = [<4, 15>] = 4/15 |
|
4/6 * (-2/5) | = | [<4, 6>] * [<-2, 5>] =
[<-8, 30>] = [<-4, 15>] = -4/15
|
Again the new construction is isomorphic to the old one such that the
properties of all operations are preserved.
Proposition 126 (Isomorphism of Rational Constructions)
Let Q' denote the old construction of the integers and Q
denote the new one. The function
is an isomorphism with respect to 0, +, -, *, ', <, i.e., i is
bijective and for all x in Q' and y in Q',
we have:
|
i(0Q') | = | 0Q, |
|
i(x+Q'y) | = | x+Qy, |
|
i(-Q' x) | = | -Q x, |
|
i(x-Q'y) | = | x-Qy, |
|
i(x*Q'y) | = | x*Qy, |
|
i(x-1) | = | x-1, |
|
i(x/Q'y) | = | x/Qy, |
|
x <= Q' y | <=> | i(x) <= Q
i(y).
|
It is easy to see that the inverse isomorphism is denoted by
where */* denotes the constructor function on Q'.
An implementation of this construction in the Logic Evaluator is shown
below,
see Appendix rational2.txt.
Real Numbers
While in Section The Real Numbers the real numbers have
been only axiomatically characterized, also a direct construction is
possible. The square of no rational number yields 2, but can define an
infinite sequence of rationals that approaches such a number
arbitrarily closely. The basic idea is to partition the set of all
"well-behaved" infinite sequences of rationals by an equivalence relation
that is true for any two sequences that approach each other arbitrarily
closely. Each such equivalence class denotes a real number with arithmetic
being defined point-wise on the sequence.
For this construction, we first define the class of "well-behaved" sequences.
Definition 111 (Cauchy-Sequence)
An infinite sequence over the reals is a
Cauchy-sequence (Cauchy-Folge), if its members approach each other
arbitrarily closely:
|
f is Cauchy-sequence:
<=> |
|
f: N -> Q /\ |
|
forall epsilon in Q>0: exists N in N: forall m >= N,
n >= N: |fm-fn| <
epsilon .
|
In other words, for every epsilon , from a certain position N on, all
members of a Cauchy-sequence stay in a "tunnel" of width epsilon :
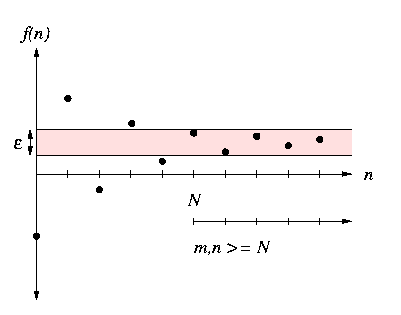
The position of this tunnel determines a real number; two sequences define the
same number if the difference of their corresponding members becomes
arbitrarily small. We define this equivalence relation and the
arithmetic operations as shown below.
Definition 112 (Real Numbers)
|
f ~ R g : <=> forall epsilon in Q>0: exists N in N: forall n >= N: |fn -
gn| < epsilon . |
|
|
|
C := {f: N -> Q: f
is Cauchy-sequence} |
|
R:= C/ ~ R |
|
|
|
0 | := | [such f in C: forall n in N: fn = 0Q] |
|
1 | := | [such f in C: forall n in N: fn = 1Q] |
|
2 | := | [such f in C: forall n in N: fn = 2Q]
|
|
x := such f in C: x =
[f]
|
|
x + y | := | [[xn +Q
yn]n] |
|
- x | := | [[-Q
xn]n] |
|
x - y | := | [[xn -Q
yn]n] |
|
x * y | := | [[xn *Q
yn]n] |
|
x-1 | := | [[xn-1]n] |
|
x / y | := | [[xn /Q
yn]n] |
|
|
|
x is positive | : <=> |
exists epsilon in Q> 0, N in N: forall n
>= N: x > epsilon |
|
x <= y | : <=> |
exists z in R: z is positive /\
x+z = y
|
We use the notation [T]n for the sequence f defined
as f(n) := T (not to confuse with the notation
[x] for the equivalence class of x). One can show that
~ R is an equivalence relation that satisfies the necessary
congruence properties to determine unique result values for the functions
defined above. Furthermore, one can show that the domain R defined in
such a way satisfies the axioms stated in Section The Real
Numbers, i.e., we have indeed the real numbers.
Complex Numbers Also C can be defined along the lines
demonstrated above. The intuition is to partition the set of all univariate
polynomials (considered as equations with righthand side zero) by the
equivalence relation that is true for two polynomials if their difference is
divisible by x2+1 (the polynomial that defines the imaginary unit).
We omit the details.
Author: Wolfgang Schreiner
Last Modification: October 4, 1999













