7.1.1 Basic Notions
Equivalence relations are binary relations that have many (but not all) of the
properties of the equality relation. First we name these properties.
Definition 98 (Relation Properties)
R is reflexive (reflexiv),
symmetric (symmetrisch),
respectively transitive (transitiv) on a set
S, if it satisfies the following properties:
|
R is reflexive on S : <=> |
|
forall x in S: <x, x> in R; |
|
R is symmetric on S : <=> |
|
forall x, y: <x, y> in R => <y, x> in R; |
|
R is transitive on S : <=> |
|
forall x, y, z: (<x, y> in R /\ <y, z> in R) => <x, z> in R.
|
Definition 99 (Equivalence Relation)
Let R be a binary relation on S.
R is an equivalence relation (Äquivalenzrelation) on S,
if it is reflexive, symmetric, and transitive on S:
|
R is equivalence relation on S: <=> |
|
R subset S x S /\ |
|
R is reflexive on S /\ |
|
R is symmetric on S /\ |
|
R is transitive on S. |
|
|
Example
- = (equality) is an equivalence relation on every set.
- Let p(x, y) : <=> x+y
is even. Then p is an equivalence relation on N.
- Let q(x, y) : <=> x mod
5 = y mod 5.
Then q is an equivalence relation on N.
- Let r(x, y) : <=> x0+y0 =
x1+y1. Then r is an equivalence relation on R x R.
- Let s(x, y) : <=> x
is parallel to (or coincides with) y. Then
s is an equivalence relation on the set of all lines in the plane.
- Let t(x, y) : <=> x
has the same age as y. Then t is an equivalence
relation on the set of all people.
The visualization of an equivalence relation by a directed graph has the
following properties:
- every node has an arrow to itself (reflexivity),
- if there is an arrow from node a to node b, then there is
also an arrow from b to a (symmetry),
- if there is an arrow from node a to node b and an arrow
from b to some node c, then there is also an arrow from a
to c (transitivity).
Example
The following graph denotes an equivalence relation:
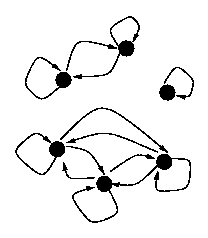
The equivalence relation imposed on the set of six nodes determines three
partitions in each of which every node is connected to every other
node. Actually, there is a close relationship between equivalence relations
and set partitions that will be elaborated later.
We demonstrate how to prove that a relation is an equivalence relation.
Proof
Let p(x, y) : <=> x+y
is even. We prove that p is an equivalence relation on N.
- p is clearly a binary relation on N.
- We prove p is reflexive on N. Take arbitrary x in N. We have to show x+x is even, i.e, 2x is even,
which clearly holds.
- We prove p is symmetric on N. Take arbitrary x in N and y in N. We assume
x+y is even. Then
y+x is even,
because x+y = y+x.
- We prove p is transitive on N. Take arbitrary x in N, y in N, and z in N. We assume
(1) x+y is even /\ y+z is even.
We have to show
(2) x+z is even
From (1), we have some a in N and b in N such that
(3) 2a = x+y /\ 2b = y+z.
Thus we know
x+z = (x+y) + (y+z) - 2y =
2a + 2b - 2y = 2(a+b-y)
such that (2) holds.
Logic Evaluator Above definitions can be implemented as
shown below, see Appendix equiv.txt.
We may construct the group of all objects that are related to some object.
Definition 100 (Class)
The class (Klasse)
of x with respect to R
is the set of all elements that are related to x by R:
|
[x]R := {y in range(R): <x, y> in R}.
|
We may just write [x], if R is clear from the context. If
R is an equivalence relation, we call [x]R the
equivalence class (Äquivalenzklasse) of x with respect to
R.
In the visualization of an (equivalence) relation by a directed graph, the
(equivalence) class of a node is the set of all nodes to which the node is
connected:
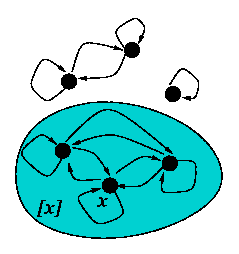
By the reflexivity of an equivalence relation, we have the following result.
Proposition 114 (Non-Empty Equivalence Classes)
If R is an equivalence relation on S, then
[x]R contains x, for every x in S:
|
forall S, R:
R is equivalence class on R => x in [x]R.
|
Example
- Let p subset N x N such that
p(x, y) <=> x+y
is even. Then we have
|
[0]p | = | {0, 2, 4, 6, 8, 10, ...}, |
|
[1]p | = | {1, 3, 5, 7, 9, 11, ...}, |
|
[2]p | = | {0, 2, 4, 6, 8, 10, ...}, |
|
[3]p | = | {1, 3, 5, 7, 9, 11, ...}, |
|
[4]p | = | {0, 2, 4, 6, 8, 10, ...}, |
|
... |
We see that [0]p union [1]p =
N and [0]p intersection [1]p =
0.
- Let q subset N x N such that
q(x, y) <=> x mod 5 = y mod 5.
Then we have
|
[0]q | = | {0, 5, 10, 15, 20, 25, ...}, |
|
[1]q | = | {1, 6, 11, 16, 21, 26, ...}, |
|
[2]q | = | {2, 7, 12, 17, 22, 27, ...}, |
|
[3]q | = | {3, 8, 13, 18, 23, 28, ...}, |
|
[4]q | = | {4, 9, 14, 19, 24, 29, ...}, |
|
[5]q | = | {0, 5, 10, 15, 20, 25, ...}, |
|
... |
We see that [0]q union [1]q
union [2]q union [3]q
union [4]q = N and that any two of these sets are
disjoint.
- Let r subset R x R such that
r(x, y) <=> x0+x1 =
y0+y1. Then we have
|
[a]r =
{b in R x R: a0+a1 =
b0+b1}
|
i.e.,
|
[a]r =
{b in R x R: b1 =
-b0+(a0+a1)}
|
If we consider R x R as the set of all points in the plane,
then [a]r denotes the line with slope
-1 that goes through a:
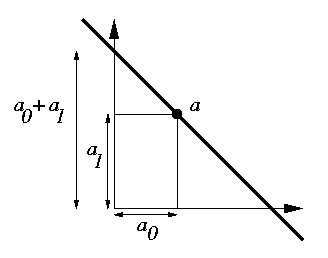
We thus have
R x R= union_a in R x R [a]r
i.e., the plane is partitioned into the set of all these lines:
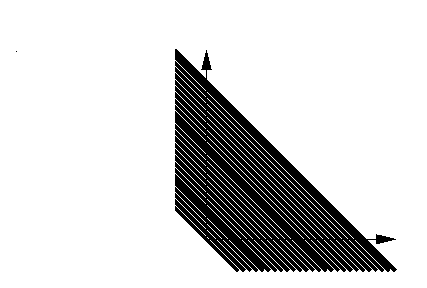
We can determine a "canonical representative" for each such line
(the point on this line whose first coordinate is zero)
and thus have
R x R= union_y in R [<0, y>]r
As illustrated by the example, different equivalences classes do not overlap.
Proposition 115 (Disjoint Equivalence Classes)
Let R be an equivalence relation on S and x and y
be elements of S. The equivalence classes of x and y with
respect to R are either identical or disjoint:
|
forall S, R:
R is equivalence relation on S => |
|
forall x in S, y in S: |
|
[x]R = [y]R \/ [x]R intersection [y]R = 0.
|
Proof
Take arbitrary S, an equivalence relation R on S, x
in S and y in S. We assume
|
(1) [x]R != [y]R, |
|
(2) [x]R intersection [y]R != 0 |
and show a contradiction. From (2), we have some z such that
|
(3) z in [x]R /\ z in [y]R.
|
We thus know
|
(4) <x, z> in R, |
|
(5) <y, z> in R.
|
We will now show
|
(6) [y]R subset [x]R, |
|
(7) [x]R subset [y]R
|
which contradicts (1).
We show (6):
From (5) and the symmetry of R, we know
From (4), (8), and the transitivity of R, we know
From (9) we know by the transitivity of R that
|
(10) forall z: <y, z> in R => <x, z> in R
|
and therefore by definition of [y]R
|
(11) forall z in [y]R: <x,
z> in R
|
and thus by definition of [x]R
|
(12) forall z in [y]R: z in [x]R
|
which gives us (6).
With the same line of reasoning, we can show (7) and are done.
As a consequence of Propositions Non-Empty Equivalence
Classes and Disjoint Equivalence
Classes, we can decompose every set S by an
equivalence relation into a set of non-empty disjoint subsets.
Definition 101 (Quotient Set)
The quotient set (Quotientenmenge) of S with respect to R
is the set of all classes induced on S by R:
Logic Evaluator
The quotient set construction can be implemented as shown below,
see Appendix equiv.txt.
We use in this example a relation on S :=
Nn x Nn whose elements are interpreted as
points in a plane. Since the computation of C := S/R
takes too long, we resort to an equivalent but faster construction C'
where a representative of each equivalence class is manually selected, and the
relation R as a set has been replaced by predicate
r. Each color in the resulting picture denotes an equivalence class on
S.
We expect this decomposition to satisfy the following properties.
Definition 102 (Partition)
D is a partition (Partitionierung) or
decomposition (Zerlegung) of S, if its elements, the
blocks (Blöcke), are non-empty and
disjoint and their union equals S:
|
D is partition of S : <=> |
|
(forall x in D: x != 0) /\ |
|
(forall x in D, y in D: x =
y \/ x intersection y = 0) /\ |
|
union D = S.
|
Example
- We define
|
A | := | {x in N: x is even}, |
|
B | := | {x in N: x > 2 /\ x
is prime}, |
|
B | := | {x in N: x is odd
/\ x is not prime}.
|
Then the set {A, B, C} is a partition of
N.
- We define
|
circle(r) := {p in R x R: p02 + p12 = r2}.
|
Then the set
is a partition of R x R as denoted by the following
picture:

The following result shows that an equivalence relation indeed defines a
partition.
Proposition 117 (Equivalence Relation Defines Partition)
Let R be an equivalence relation on S. The quotient
set of S with respect to R is a partition of S:
|
forall S, R:
R is equivalence relation on S => |
|
S/R is partition of S.
|
Proof
Take arbitrary S and equivalence relation R on S. We show
S/R is a partition of S:
- Take arbitrary x in S/R. By definition of
S/R, we have some a in S such that
x = [a]R. By
Proposition Non-Empty Equivalence Classes, a
in [a]R, therefore x != 0.
- Take arbitrary x in S/R and
y in S/R.
By definition of
S/R, we have some a in S and b
in S such that
x = [a]R and y = [b]R.
By Proposition Disjoint Equivalence Classes,
[a]R = [b]R \/ [a]R intersection [b]R = 0.
- By definition of S/R, union S/R
subset S. We show S subset union S/R.
Take arbitrary x in S. Then from
Proposition Non-Empty Equivalence Classes
we have x in [x]R and from the definition of
S/R we have
[x]R in S/R, thus x in union S/R.
We can also proceed in the other direction and construct a relation from a
partition.
Definition 103 (Induced Relation)
The relation induced by a partition D is the set of all pairs of
elements of the same block of D:
|
x ~ D y : <=> exists d in D: x in d /\ y in d.
|
The constructed relation is an equivalence relation.
Proposition 119 (Partition Defines Equivalence Relation)
Let D be a partition of S.
The relation induced by D is an equivalence relation
on S:
|
forall S, D:
D is partition of S => |
|
~ D is equivalence relation on S.
|
Proof
Take arbitrary S and partition D on S. We show that
~ D is an equivalence relation on S.
- Binary Relation
- By definition, ~ D is a binary
relation. If x ~ D y, then we have
some d in D such that
x in d and y in d. Since union D = S, we have x in S and y
in S and ~ D is a relation on S.
- Reflexivity
-
Take arbitrary x in S. Since union D =
S, we have some d in D such that x in d and thus x ~ D x.
- Symmetry
-
Take arbitrary x in S and
y in S and assume x ~ D
y. Then we have some d in D such that x
in d /\ y in d which gives us
y ~ d x.
- Transitivity
- Take arbitrary x in S,
y in S, and z in S and assume
x ~ D y and
y ~ D z. Then we have some
d in D such that x
in d /\ y in d and some
e in D such that y
in d /\ z in d.
Since y in d and y in e,
Proposition Disjoint Equivalence Classes gives us
d = e and thus x ~ D z.
As shown above, equivalence relations and partitions are just different
notions for the same concept; we can always construct from one description the
other one. Actually, each construction is the inverse of the other one as
stated by the following result (which can be easily proved).
Proposition 121 (Equivalence Relations and Partitions)
Let R be an equivalence relation on S. Then R is the
relation induced by the quotient set of S with respect to R:
|
forall S, R:
R is equivalence relation on S => |
|
R = ~ S/R.
|
Let D be a partition of S. Then D is the quotient set of
the relation induced by D:
|
forall S, D:
D is partition of S => |
|
D = S/ ~ D.
|
Logic Evaluator We can implement the new notions as shown
below, see Appendix
equiv.txt.
The partitioning of sets into equivalence classes is an important methodology
with many applications some of which are demonstrated in the following
subsections.
Author: Wolfgang Schreiner
Last Modification: October 4, 1999













