6.5 Special Functions
We now investigate the behavior of several important functions over
R. Most of the notations defined for sequences in the
previous section (monotonicity, upper and lower bound, supremum, infimum,
convergence, limit) apply to such functions as well; we do not repeat the
corresponding definitions.
Real functions can be constructed in a
modular manner by composing more complex functions from simpler ones. The
composition operations are defined "pointwise", i.e., the value of a
composed function at point x is determined only by the values of the
component functions at this point.
Definition 87 (Pointwise Function Definition)
Let RealFun = R -> R.
We define the following function composition operations:
|
. : R -> RealFun |
|
c(x) := c; |
|
|
|
+: (RealFun x RealFun) -> RealFun |
|
(f+g)(x) := f(x) + g(x); |
|
|
|
-: (RealFun x RealFun) -> RealFun |
|
(f+g)(x) := f(x) - g(x); |
|
|
|
: (RealFun x RealFun) -> RealFun |
|
(f*g)(x) := f(x) * g(x); |
|
|
|
./.: (RealFun x RealFun) -> (R ->partial R) |
|
(f/g)(x) :=
f(x)/g(x); |
|
|
|
..: (RealFun x Z) -> (R ->partial R) |
|
(fn)(x) := f(x)n; |
|
|
|
sqrt ( ): (Z x RealFun) -> (R ->partial R) |
|
(sqrtn(f))(x) := sqrtn(f(x));
|
The first composition operation makes a function from a constant, e.g., the
number 5 can be interpreted as the constant function 5(x) := 5. The
domain of a quotient function f/g is the set of all reals
x such that g(x) != 0. The domain of
fn and of sqrtn(f) is R, if
n >= 0. Otherwise, their domain is the set of all reals x
such that f(x) > 0.
Example
- Let f(x) := 2x2 and g(y) :=
y+4. Then,
for every x in R,
(sqrt(f+g))(x) = sqrt(2x2 + x + 4).
- The function
f(x) := 3x2+xsqrt(x)
equals
3*g+h
where g(x) := x2 and h(x) =
xsqrt(x).
- The function
1R2+sqrt( )/1R+1 equals the
function
f(x) := x2+sqrt(x)/x+1.
Integer Functions
Various functions map real numbers to integers.
Definition 88 (Floor and Ceiling)
The floor of a real number x is the largest integer less than or
equal x.
floor(x) := max {y in Z: y <= x}.
Analogously, the ceiling of x is the
smallest integer greater than or equal x:
ceiling(x) := min {y in Z: y >= x}.
In above definition, we consider Z as a subset of R (instead of
writing h(Z) where h is the homomorphism that
actually maps Z into R).
The graphs of these functions are depicted by the following diagram (with the
floor denoted by a solid line and the ceiling denoted by the dotted line):
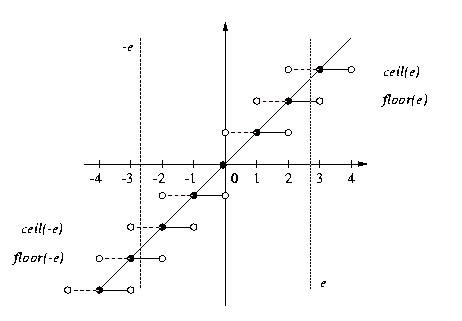
We see that the floor function lies on or below the first diagonal while the
ceiling lies above the diagonal. If we shift the diagonal line down one unit,
it lies completely below the floor function; if we shift it up one unit, it
lies completely above the floor function. Furthermore, functions intersect
with each other at the diagonal exactly for the integer points. Finally, the
functions are reflections of each other about both axes. We thus have the
following three results.
Proposition 93 (Floor and Ceiling)
For every x in R, we have:
|
x-1 < floor(x) <= x <= ceiling(x) < x+1, |
|
floor(x) = x <=> x in Z <=> ceiling(x) = x, |
|
floor(-x) = -ceiling(x), ceiling(-x) = -floor(x).
|
(We use in above proposition A <=> B <=> C to
denote (A <=> B) /\ (B <=> C)).
Furthermore, we have the following property that allows us to shift integer
terms out of a floor or a ceiling.
Proposition 94 (Floor and Ceiling Shifts)
For every x in R and i in Z, we have:
|
floor(x+i) = floor(x)+i, |
|
ceiling(x+i) = ceiling(x)+i.
|
Please note that above rule does not hold for multiplication, i.e., there
exist x in R and i in Z such that
floor(x*i) != floor(x)*i (e.g.,
2*floor(0.5) = 0 != 1 = floor(2*0.5)).
The following rules help us to get rid of the floor and ceiling brackets under
certain circumstances.
Proposition 95 (Floor and Ceiling Removal)
For every x in R and i in Z, we have:
|
x < i | <=> | floor(x) < i, |
|
i < x | <=> | i < ceiling(x), |
|
x <= i | <=> | ceiling(x) <= i, |
|
i <= x | <=> | i <= floor(x).
|
Computer languages and pocket calculators sometimes provide operations to
truncate the fractional part of a number.
Proposition 96 (Truncation)
The truncated part (abgeschnittener Teil) of a real number is the number
without its fractional part:
|
trunc(x) :=
if x < 0 then ceiling(x) else floor(x).
|
For this function, we have the following result.
Proposition 97 (Truncation)
For every x in R, the truncated part of the negation of
x is the negation of the truncated part of x:
forall x in R: trunc(-x) =
-trunc(x).
Apart from that, truncation does not have many nice mathematical properties
(as we have for floor and ceiling), therefore it is rarely used in
mathematical practice. A number of other interesting functions can be defined
with the help of floor and ceiling.
Example
The graph of f(x) := x-floor(x) is depicted by
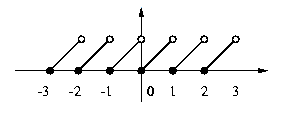
The graph in above example is an infinite replication of the graph in the
interval [0, 1[, i.e., the corresponding function has period 1.
Definition 89 (Periodic Functions)
A function has period (Periode) a, if the function values are
repeated in intervals of width a:
|
f has period a : <=> |
|
f: R -> R /\ a in R /\ forall x in R: f(x+a) =
f(x).
|
A function is periodic (periodisch) if it has some period:
|
f is periodic : <=> exists a in R: f has period a.
|
With the help of the floor function, we can also perform "integer division"
(see Proposition Integer Operations) of two reals x and y as
floor(x/y). A corresponding remainder operation is then
defined as follows.
Definition 90 (Real Remainder)
|
mod: (R x R) -> R |
|
x mod y := x -
y*floor(x/y).
|
As an immediate consequence of this definition, we have, for every x
in R and y in R with y != 0,
x = y*floor(x/y) + x mod
y.
For positive x and y, the intuitive meaning of integer quotient and
remainder in R can be easily grasped by imagining a circle of
circumference y on which we travel from a denoted starting point
distance x:
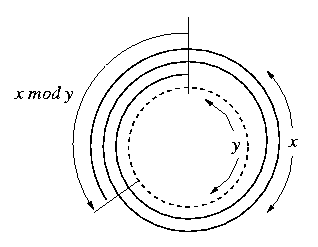
The number of times that we traverse the circle is
floor(x/y), the distance of the final point from the starting
point is x mod y.
Example
- floor(5.44/4) = 1; 5.44 mod 4 = 5.44 - 4*1 = 1.44.
- floor(-5.44/4) = -2; -5.44 mod 4 = -5.44 - 4*(-2) =
2.56.
- floor(5.44/-4) = -2; 5.44 mod -4 = 5.44 - (-4)*(-2) =
-2.56.
- floor(-5.44/-4) = 1; -5.44 mod -4 = -5.44 - (-4)*1 =
-1.44.
From above examples, we realize the following facts about the remainder
operation.
Proposition 98 (Remainder Laws)
For every x in R and y in R, we have
|
y > 0 => (0 <= x mod y < y),
|
|
y < 0 => (0 >= x mod y > y).
|
Polynomial Functions and Rational Functions
Functions may be defined by polynomials.
Definition 91 (Polynomial Function)
For every n >= 0 and a: Nn+1 -> R, we
call p: R -> R,
p(x) := (sum0 <= i <= n aixi)
a polynomial function (Polynomfunktion) of degree n
with coefficients a:
|
p is polynomial function of degree n
with coefficients a : <=> |
|
n in N /\ a:
Nn+1 -> R /\ |
|
forall x in R: p(x) = (sum0 <= i <= n a</sub>i); |
|
p is polynomial function : <=> |
|
exists n in N, a: p
is polynomial function of degree n
with coeff. a; |
|
degree(p) :=
such n in N: exists a: Nn+1 in R: |
|
p is polynomial function of degree n
with coefficients a; |
|
coefficients(p) :=
such a: exists n in N: |
|
a: Nn+1 in R /\ |
|
p is polynomial function of degree n
with coefficients a. |
|
|
Degree and coefficients of a polynomial function are uniquely defined (which
we do not show here). Every polynomial function can be pointwise defined from
identity and constant functions just by use of +, -, * and
exponentiation (with non-negative exponents); vice versa, any function defined
in such a way is a polynomial function.
Example
- The constant function (konstante Funktion) f(x) :=
c (for any c in R) is a polynomial function of
degree 0 and with coefficients [c].
- The linear function (lineare Funktion) f(x) :=
ax+b (for any a in R and b
in R) is a polynomial function of degree 1 with coefficients
[a, b].
-
The square function (Quadratfunktion) f(x) :=
x2 is a polynomial function of degree 2 with coefficients [1, 0,
0].
- f(x) := x5-3x2+1 is a polynomial
function with degree 5 and coefficients [5, 0, 0, -3, 0, 1].
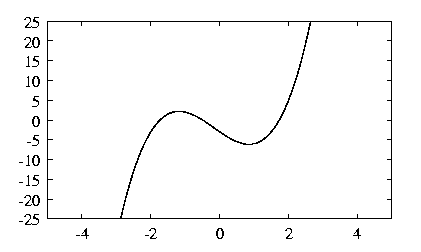
- The function f(x) := (2x+1)*(x2-3) is a
polynomial function because it can be represented (by simplification of
the defining term) as
It thus is of degree 3 and has coefficients <2, 1, -6, -3>.
Every polynomial function has a function graph with a single "smooth" path
such as the graph for the function in the last last example:
By allowing also division as a function composition operation, we get the
following class of real functions:
Definition 92 (Rational Function)
For every pair of polynomial functions p and q, we call
the function
r: R -> R, r(x) :=
p(x)/q(x) with R := R-
{x in R: q(x) = 0} a rational
function (rationale Funktion):
|
r is a rational function : <=> exists p, q: |
|
p is polynomial function /\ |
|
q is polynomial function /\ |
|
forall x in R: r(x) =
p(x)/q(x).
|
Example
- The reciprocal function (Reziprokfunktion) f(x) :=
1/x is a rational function with domain R- {0}.
- f(x) := 3x2-2x+1/x2+1
is a rational function with domain R.
- f(x) := 3x2-2x+1/x2-1
is a rational function with domain R- {-1,1}.
Rational functions may have function graphs with multiple paths separated by
those horizontal coordinates where the denominator becomes zero; e.g. for
the rational function in the last example we have:
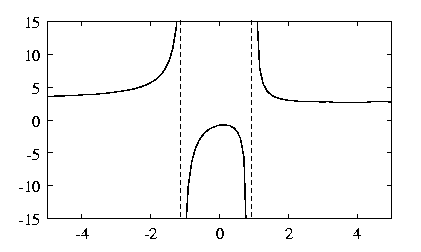
The dashed lines denote the discontinuities at -1 and 1 where the rational
function is not defined.
Exponentiation and Natural Logarithm
The sequence [ei]i (where e denotes Euler's
number) can be smoothly extended to a function over R.
Definition 93 (Exponential Function and Logarithm Function)
|
exp: R -> R> 0 |
|
exp(x) :=
(sumi=0 oo xi/i!);
|
|
|
ln: R> 0 -> R |
|
ln(x) := exp-1(x).
|
|
One can show that, for every x in R,
[(sum0 <= i <= n xi/i!)]n converges
and that exp(x) is thus well defined. Furthermore, the
function is bijective and thus, for every x > 0,
ln(x) is well-defined. The graphs of both functions are
depicted as follows:
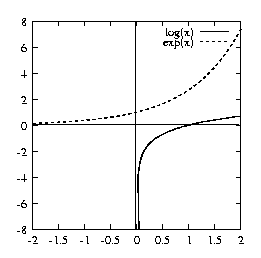
where we see for instance exp(0) = 1 and ln(1) = 0. More
general, we have the following properties.
Proposition 99 (Exponential and Logarithm Properties)
For every x in R and y in R, we have:
|
exp(x+y) | = | exp(x) *
exp(y), |
|
exp(x-y) | = | exp(x) /
exp(y), |
|
exp(-x) | = | 1/exp(x), |
|
exp(x*y) | = | exp(x)y, |
|
exp(0) | = | 1, |
|
exp(1) | = | e,
|
|
|
ln(x*y) | = | ln(x)+ln(y),
|
|
ln(x/y) | = |
ln(x)-ln(y),
|
|
ln(1/x) | = |
-ln(x),
|
|
ln(xy) | = | y*ln(x), |
|
ln(e) | = | 1, |
|
ln(1) | = | 0. |
|
|
|
|
Proof
Take arbitrary x in R and y in R.
We show
exp(x+y) = exp(x) *
exp(y).
We have
|
exp(x+y) | = | |
|
((sumi=0 oo xi/i!)) +
((sumi=0 oo yi/i!)) | = | |
|
(sumk=0 oo
(sum0 <= i <= k xi/i!
yk-i/(k-i)!)) | = | |
|
(sumk=0 oo
1/k!
(sum0 <= i <= k
k!/i!(k-i)!
xiyk-i)) | = | |
|
(sumk=0 oo
1/k!
(sum0 <= i <= k
(k i)
xiyk-i)) | = | (*) |
|
(sumk=0 oo (x+y)k/k!)
| = | |
|
exp(x)+exp(y).
|
(*) The fact (sum0 <= i <= k
(k i)
xiyk-i) =
(x+y)k has to be shown in a separate proof (by
induction over k).
Most properties about exponentiation are easy consequences of the first fact
in above proposition, e.g. we have, for every x in R,
exp(0) = exp(x + 0) =
exp(x)*exp(0)
and consequently exp(0) = 1. Properties of the logarithm
are direct consequences of its definition as the inverse of exponentiation.
Proof
Take arbitrary x in R and y in R.
We show
ln(x*y) = ln(x)+ln(y).
We have
|
ln(x) + ln(y) | = | |
|
ln(exp(ln(x) + ln(y))) | = | |
|
ln(exp(ln(x)) *
exp(ln(y))) | = | |
|
ln(x * y).
|
On the basis of "exp" and "ln" a more general kind of exponentiation and
logarithm can be defined.
Definition 94 (General Exponentiation and Logarithm Function)
|
exp: (R>0 x R) -> R> 0 |
|
expa(x) :=
exp(x*ln(a)),
|
|
|
log: (R>0 x R> 0) -> R |
|
loga(x) :=
ln(x)/ln(a).
|
|
Both functions are the inverse of each other, e.g. we have
for every a in R> 0 and x in R> 0
expa(loga(x)) =
expa(ln(x)/ln(a)) =
(ln(x)/ln(a)*ln(a) = x.
The graphs of generalized exponentiation and logarithm look like their basic
counterparts but are scaled by a constant factor ln(a).
Trigonometric Functions
The trigonometric functions are defined as limits of some power series.
Definition 95 (Trigonometric Functions)
The functions sine (Sinus), cosine (Cosinus),
tangent (Tangens), and cotangent (Cotangens) are defined
as follows:
|
sin: R -> [-1,1] |
|
sin(x) :=
(sumi=0 oo (-1)kx2k+1/(2k+1)!);
|
|
|
cos: R -> [-1,1] |
|
cos(x) :=
(sumi=0 oo (-1)kx2k/(2k)!);
|
|
|
|
|
tan: R ->partial R |
|
tan(x) :=
sin(x)/cos(x);
|
|
|
cot: R ->partial R |
|
cot(x) :=
cos(x)/sin(x).
|
|
|
The function graphs of sine and cosine are depicted as follows:

We see that the sine is zero for every multiple of pi and alternates
between its maximum +1 and minimum -1 at the points in the middles
between; the function has period 2 pi . The cosine is just a copy of the
sine shifted by pi /2 to the left.
Proposition 102 (Sine and Cosine Values)
For all i in Z, we have:
|
sin(2 pi i) | = | 0, |
|
sin(2 pi i+ pi /2) | = | 1, |
|
sin(2 pi i+ pi ) | = | 0, |
|
sin(2 pi i+3 pi /2) | = | -1, |
|
|
|
|
cos(2 pi i) | = | 1, |
|
cos(2 pi i+ pi /2) | = | 0, |
|
cos(2 pi i+ pi ) | = | -1, |
|
cos(2 pi i+3 pi /2) | = | 0.
|
|
|
Many properties of sine and cosine can be derived from the following
fundamental proposition (which we state without proof).
Proposition 103 (Sine and Cosine)
For every x in R and y in R, we have
|
sin(x + y) | = |
sin(x)*cos(y) +
cos(x)*sin(y), |
|
cos(x + y) | = |
cos(x)*cos(y) -
sin(x)*sin(y).
|
We then have the following results.
Proposition 104 (Sine and Cosine)
For every x in R and y in R, we have:
|
sin(x+2 pi ) | = | sin(x), |
|
sin(x+ pi /2) | = | cos(x), |
|
sin( pi /2-x) | = | cos(x), |
|
sin(-x) | = |
-sin(x), |
|
sin(2x) | = | 2sin(x)cos(x),
|
|
|
cos(x+2 pi ) | = | cos(x), |
|
cos(x+ pi /2) | = | -sin(x), |
|
cos( pi /2-x) | = | -sin(x), |
|
cos(-x) | = | cos(x), |
|
cos(2x) | = | cos2(x)-sin2(x).
|
|
cos2(x)+sin2(x) = 1,
2 sin(x)*sin(y) =
cos(x-y) - cos(x+y),
2 cos(x)*cos(y) =
cos(x-y) + cos(x+y),
2 sin(x)*cos(y) =
sin(x-y) + sin(x+y).
Proof
Take arbitrary x in R. We show
sin(x+2 pi ) = sin(x).
We have
|
sin(x+2 pi ) =
sin(x)*cos(2 pi )+cos(x)*sin(2 pi ) |
|
= sin(x)*1+cos(x)*0 = sin(x).
|
The function graphs of tangent and cotangent look as follows:
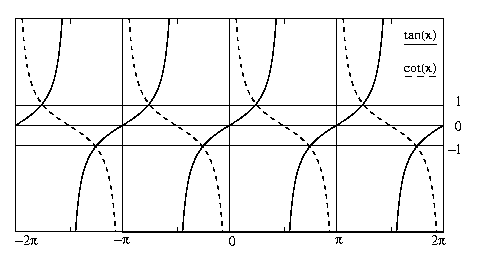
The tangent function has period pi , its value is 0 at every multiple of
pi and undefined at every odd multiple of pi /2; furthermore
the function is unbounded in both directions. The cotangent is the tangent
horizontally flipped and shifted left by pi /2. Both functions
meet at odd multiples of pi /4 at values +/-1.
Proposition 106 (Tangent and Cotangent Values)
For all i in Z, we have:
|
tan( pi i) | = | 0, |
|
tan( pi i+ pi /4) | = | 1, |
|
tan( pi i- pi /4) | = | -1, |
|
|
|
|
cot( pi i+ pi /2) | = | 0, |
|
cot( pi i+ pi /4) | = | 1, |
|
cot( pi i- pi /4) | = | -1. |
|
|
|
|
Many properties of tangent and cotangent can be derived from the following
proposition (which we state without proof).
Proposition 107 (Tangent and Cotangent)
For every x in R and y in R, we have
tan(x+y) =
tan(x)+tan(y)/1-tan(x)*tan(y),
cot(x+y) =
cot(x)*cot(y)-1/cot(x)+cot(y).
We than also have the following results.
Proposition 108 (Tangent and Cotangent Properties)
For every x in R and y in R, we have:
|
tan(-x) | = | -tan(x), |
|
tan(x) | = | -cot(x+ pi /2),
|
|
|
cot(-x) | = | -cot(x), |
|
tan(x) | = | -tan(x- pi /2).
|
|
|
Proof
Take arbitrary x in R. We show
tan(-x) = - tan(x).
We have tan(-x) =
sin(-x)/cos(-x) =
-sin(x)/cos(x) =
-sin(x)/cos(x) =
-tan(x).
Author: Wolfgang Schreiner
Last Modification: October 4, 1999













