2.3 Predicate Logic
Propositional logic is just concerned about the composition of formulas; it
does not investigate the properties described by these formulas. We now enter
the realm of predicate logic that is able to describe objects and
properties of a domain, i.e., of some abstract model of the real
world.
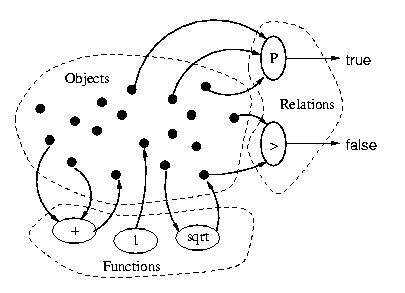 A Domain
A Domain
Definition 11 (Domain) A domain (Bereich)
or structure (Struktur) consists of
- A collection of values (Werte) or objects (Gegenstände);
the number of objects may be finite or infinite (but not zero).
- A collection of functions (Funktionen), also called
mappings (Abbildungen, Zuordnungen); each function takes a certain
number of values, the arguments (Argumente), and returns a value, the
result (Resultat, Ergebnis). The number of arguments is the
arity of the function.
A function with arity 0 is also called a constant (Konstante).
- A collection of predicates (Prädikate), also called
relations (Relationen, Beziehungen), properties (Eigenschaften),
attributes (Attribute); each predicate takes a certain number of
values, the predicate arguments, and returns a truth value.
If the predicate returns true, it is said to be true, to
hold (halten), or to be valid (gültig) for these values.
Example
Various examples of domains are
- the set of natural numbers as values with constants "zero" and
"one" and functions "addition", "multiplication", and predicate "is
less than';
- the people in Austria as "values" with functions "mother of" and
"father of" and predicates, "is male", "is female", "are parents of";
- the set of Java values of type
int[] and int with
function "indexed array access" and predicate "is sorted".
Predicate logic can be considered an extension of propositional logic, i.e.,
all propositional logic formulas are also predicate logic formulas and all
properties derived for propositional logic also hold (in a generalized form)
in predicate logic. While in propositional logic the only elementary formulas
are the logical constants `T' and `F', predicate logic allows elementary
formulas that express properties of objects. For this purpose, predicate logic
introduces means to denote objects in a given domain.
Author: Wolfgang Schreiner
Last Modification: October 4, 1999













