Tutorials

The following tutorials are offered on ISSAC 2004

1. Cylindrical Algebraic Decomposition by Christopher W. Brown
2. Power Series and Summation by Wolfram Koepf

The tutorials will take place on Sunday July 4, 2004.
Tutorial fee rates are announced on the Registration Information Page.

Tutorial 1

Cylindrical Algebraic Decomposition
Christopher W. Brown
U.S. Naval Academy

A formula comprised of boolean combinations of polynomial equalities and inequalities in n variables defines a geometric object in a natural way - the object consists of those points in n-dimensional Euclidean space that satisfy the formula.¹ Such geometric objects, called semi-algebraic sets, are omnipresent in science, mathematics and engineering, and the question of how to compute with them symbolically is a natural and fundamental one for our community to consider. This tutorial presents Cylindrical Algebraic Decomposition (CAD), which provides a powerful tool for carrying out many such computations.

CAD arose from interest in quantifier elimination. The quantifier elimination problem considers a formula comprised of boolean combinations of polynomial equalities and inequalities in which some variables are quantified, and asks for a quantifier-free formula that is logically equivalent over the reals.² That a quantifier-free equivalent formula always exists was proven by Alfred Tarski in the 1930's by giving the first quantifier elimination algorithm. In the 1970's, George Collins developed CAD as the basis of a new and much more efficient algorithm for quantifier elimination. Improvements in his algorithm and applications of it to various problem domains have been a subject of research ever since. Currently there are implementations of CAD and quantifier elimination by CAD in Reduce, as stand-alone C/C++ applications, and as part of Mathematica 5.

Essentially, CAD gives a representation for semi-algebraic sets - an alternative to representing them by formulas. Many operations or queries that are difficult in the formula representation are easy in the CAD representation. One such operation is the projection of an object onto a lower dimensional space. This corresponds exactly to eliminating existentially quantified variables from the formula defining the object, which is the connection between CAD and quantifier elimination. Many other operations that are difficult in the formula representation - determining dimension, for example - are easy in the CAD representation, and some of these other operations along with problems they help solve are also addressed in this presentation. The general topic outline for the tutorial is as follows:

1. Semi-algebraic sets, Cylindrical Algebraic Decomposition (CAD), and converting between formulas and CADs.
2. Quantifier elimination using CADs.
3. Formula simplification using CADs.
4. Survey of the current state of the art in constructing CADs.
5. Survey of recent work in applying CADs, including specializing CAD for particular applications.

This presentation is intended to be accessible to people with diverse mathematical backgrounds - from people who are familiar only with basic commutative algebra to people who are knowledgeable about quantifier elimination and even CAD. It aims to develop CAD from a novel viewpoint, with a particular eye towards communicating the geometric intuition behind it, which will hopefully provide a fresh look at the subject for those who are already familiar with CAD, and a good foundation for those who are not. Finally, the survey of CAD applications and specialization should be useful for anyone interested in using CAD or of improving it.

1. Some formulas and the semi-algebraic sets (in blue) they define.

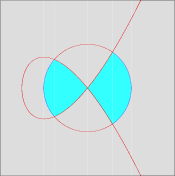x2 + y2 ≤ 1	2 y2 < x2 (2 x + 3)	x2 + y2 ≤ 1 ∧ 2 y2 < x2 (2 x + 3)

2. Some quantified formulas and quantifier-free equivalents.

• ∃ x [a ≠ 0 ∧ a x² + b x + c = 0]   ⇔   b² - 4 a c ≥ 0
• ∃ x,y [ y = m x + k ∧ x² + y² = 1 ]   ⇔   k² - m² - 1 ≤ 0

Tutorial 2

Power Series and Summation
Wolfram Koepf
University of Kassel, Germany

15 years ago Doron Zeilberger's seminal work revolutionized algorithmic summation ([4],  [6]). Briefly afterwards an algorithm for the computation of infinite series of hypergeometric functions was published [3]. The algorithms under consideration are too complicated for hand computations and therefore require implementations. Several implementations of the basic algorithms of Gosper [1], Zeilberger [7], Petkovsek [5] and Koepf [2], [3] were developed. This software development is still ongoing, and not all questions of efficiency are completely resolved.

The above algorithms have many applications in combinatorics since most combinatorial quantities have representations as sums. If such a sum is hypergeometric, Zeilberger's algorithm either finds a "closed form" or detects a holonomic recurrence equation for it. A homogeneous linear recurrence equation with polynomial coefficients is called holonomic.

Other combinatorial problems are solved with the use of generating functions. Mostly one is interested in a "closed form" representation of the coefficients, or one would like to compute the coefficients efficiently. This can be handled by Koepf's algorithm, again by computing a holonomic recurrence equation. Where required, both in Zeilberger's as well as in Koepf's case Petkovsek's algorithm decides whether such a term can be represented in "closed form", namely as hypergeometric term. There are generalizations of the algorithms for basic hypergeometric series, for multiple sums, for integrals instead of sums, and one can compute holonomic differential equations [4].

The following algorithms are covered in the tutorial:

• the computation of power series representations of hypergeometric type functions, given by "expressions" (like arcsin(x)/x)
• the computation of holonomic differential equations for functions, given by expressions
• the computation of holonomic recurrence equations for sequences, given by expressions (like binomial(n,k)*x^k/k!)
• the computation of generating functions
• the computation of antidifferences of hypergeometric terms (Gosper's algorithm)
• the computation of holonomic differential and recurrence equations for hypergeometric series, given the series summand (like P(n,x)=sum(binomial(n,k)*binomial(-n-1,k)*((1-x)/2)^k,k=0..n)) (Zeilberger's algorithm)
• the computation of hypergeometric term representations of series (Zeilberger's and Petkovsek's algorithm)
• the verification of identities for (holonomic) special functions.

All algorithms are presented by Maple implementations.

References

1. Gosper Jr., R. W.: Decision procedure for indefinite hypergeometric summation. Proc. Natl. Acad. Sci. USA 75, 1978, 40-42.
2. Gruntz, D., Koepf, W.: Maple package on formal power series. Maple Technical Newsletter 2 (2), 1995, 22-28.
3. Koepf, W.: Power series in computer algebra. J. Symbolic Computation 13, 1992, 581-603.
4. Koepf, W.: Hypergeometric summation. Vieweg, Braunschweig-Wiesbaden, 1998.
5. Petkovsek, M.: Hypergeometric solutions of linear recurrences with polynomial coefficients. J. Symbolic Computation 14, 1992, 243-264.
6. Petkovsek, M., Wilf, H. and Zeilberger, D.: A=B. AK Peters, Wellesley, 1996.
7. Zeilberger, D.: A fast algorithm for proving terminating hypergeometric identities. Discrete Math. 80, 1990, 207-211.

Tutorials Chair

Thomas Sturm

(University of Passau, Germany)